第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
8. 如图,$AB\perp AC$于点$A$,$BD\perp CD$于点$D$。若$AC = DB$,则下列结论不正确的是(
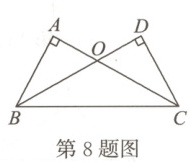
A.$\angle A = \angle D$
B.$\angle ABC = \angle DCB$
C.$OB = OD$
D.$OA = OD$
C
)
A.$\angle A = \angle D$
B.$\angle ABC = \angle DCB$
C.$OB = OD$
D.$OA = OD$
答案:
8.C
9. 如图,在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,在$AC$和$AB$上分别截取$AE$,$AD$,使$AE = AD$。再分别以点$D$,$E$为圆心,大于$\frac{1}{2}DE$长为半径作弧,两弧在$\angle BAC$内交于点$F$,作射线$AF$交边$BC$于点$G$。若$CG = 4$,$AB = 12$,则$\triangle ABG$的面积为(
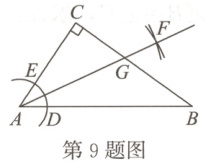
A.12
B.24
C.30
D.48
B
)
A.12
B.24
C.30
D.48
答案:
9.B
10. 如图,在$\triangle AOB$和$\triangle COD$中,$OA = OB$,$OC = OD$,$OA < OC$,$\angle AOB = \angle COD = 36^{\circ}$。连接$AC$,$BD$交于点$M$,连接$OM$。有下列结论:①$\angle AMB = 36^{\circ}$;②$AC = BD$;③$OM$平分$\angle AOD$;④$MO$平分$\angle AMD$。其中正确结论的个数有(
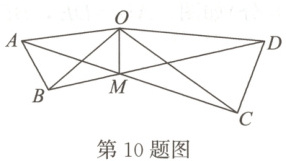
A.1个
B.2个
C.3个
D.4个
C
)
A.1个
B.2个
C.3个
D.4个
答案:
10.C
11. 如图,$AC = AD$,$\angle 1 = \angle 2$,要使$\triangle ABC\cong\triangle AED$,应添加的一个条件是
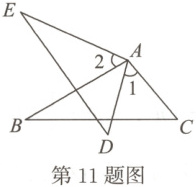
∠E=∠B(答案不唯一)
。(只需写出一个即可)
答案:
11.∠E=∠B(答案不唯一)
12. 如图,已知$AB// CF$,$E$为$AC$的中点。若$FC = 8cm$,$DB = 4cm$,则$AB =$
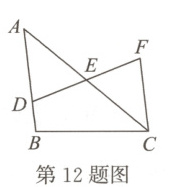
12
$cm$。
答案:
12.12
13. 如图,在平面直角坐标系中,已知$\triangle AOB\cong\triangle COD$,则点$D$的坐标是
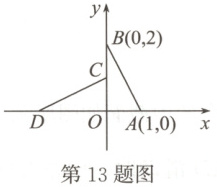
(-2,0)
。
答案:
13.(-2,0)
14. 如图,$AD$是$\triangle ABC$中$\angle BAC$的平分线,$DE\perp AB$于点$E$,$S_{\triangle ABC} = 10$,$DE = 2$,$AB = 6$,则$AC$的长是
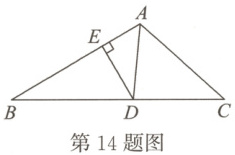
4
。
答案:
14.4
15. 如图,$AE\perp AB$且$AE = AB$,$BC\perp CD$且$BC = CD$。请按照图中所标注的数据,计算图中实线所围成的图形的面积$S$是
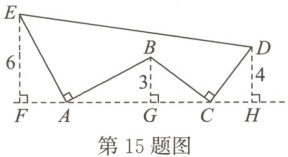
50
。
答案:
15.50
查看更多完整答案,请扫码查看


