《2025年单元质量达标八年级数学上册人教版》

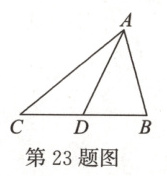
23. （11分）如图，在△ABC中，AD是中线。
（1）求证：AB + AC ＞ 2AD；
（2）若AB = 5，AC = 7，求AD长的取值范围。

答案：
23.
(1)证明:如图，延长AD至点E，使ED=AD，连接CE。
　
∵AD是△ABC的中线，
　
∴BD=CD。
在△ABD和△ECD中，$\begin{cases} BD = CD, \\ \angle ADB = \angle EDC, \\ AD = ED, \end{cases}$
　
∴△ABD≌△ECD(SAS)。
　
∴AB=EC。
　　　　在△ACE中,AC+EC＞AE,
　
∴AC+AB＞2AD。
(2)在△ACE中,AC−CE＜AE＜AC+CE,
　
∴AC−AB＜2AD＜AC+AB，即$\frac{7−5}{2}$＜AD＜$\frac{7+5}{2}$。
　
∴1＜AD＜6。
　

24. (14分)在数学实验课上，老师让学生以“折叠筝形”为主题开展数学实践探究活动。定义：两组邻边分别相等的四边形叫作筝形。
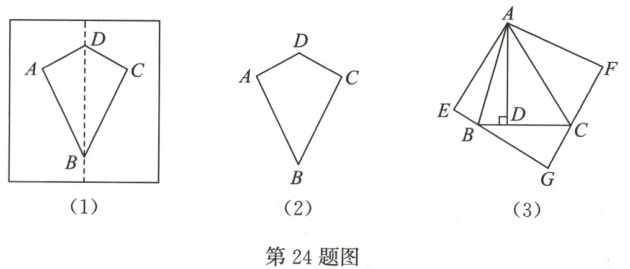
(1)概念理解：如图(1)，将一张纸对折压平，以折痕为边折出一个三角形，然后把纸展平，折痕为四边形ABCD。判断四边形ABCD的形状：是筝形。(填“是”或“不是”)
(2)性质探究：如图(2)，已知四边形ABCD纸片是筝形，请用测量、折叠等方法猜想筝形的角、对角线有什么几何特征，然后写出一条性质并进行证明。
(3)拓展应用：如图(3)，AD是锐角三角形ABC的高，将△ABD沿边AB翻折后得到△ABE，将△ACD沿边AC翻折后得到△ACF，延长EB，FC交于点G。若∠BAC = 50°，当△BCG是等腰三角形时，求∠BAD的度数。

答案：
24.
(1)是
(2)解:
　　性质:在筝形中，较长的对角线平分较短的对角线所对的两个角。
　　证明:如图，连接BD，AC。
∵四边形ABCD是筝形，
∴AD=CD,AB=CB。
∵在△ABD和△CBD中，$\begin{cases} AD = CD, \\ AB = CB, \\ BD = BD, \end{cases}$
∴△ABD≌△CBD(SSS)。
∴∠ADB=∠CDB,∠ABD=∠CBD。
∴BD平分∠ABC，DB平分∠ADC。
　
(3)解:由折叠的性质，得∠BAD=∠BAE，∠CAD=∠CAF，∠E=∠ADB=∠F=90°。
∵∠BAC=∠BAD+∠CAD=50°,
∴∠EAF=2∠BAC=100°。
∴∠EGF=360°−∠E−∠F−∠EAF=80°
　　当BC=BG时，∠BCG=∠BGC=80°,
∴∠ACB=∠ACF=$\frac{1}{2}$(180°−∠BCG)=50°。
∴∠ABC=180°−∠ACB−∠BAC=80°。
∵∠ADB=90°,
∴∠BAD=90°−∠ABC=10°。
　　当BC=CG时，同理可得∠BAD=40°。
　　当GC=BG时，同理可得∠BAD=25°。
　　综上所述，当△BCG是等腰三角形时，∠BAD的度数为10°或25°或40°。