第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
22.(本题满分12分)
一辆货车从仓库O出发在东西方向的街道上运送水果,规定向东为正方向,货车到达的5
个销售地点依次为A,B,C,D,E,最后回到仓库O,货车行驶的距离记录(单位:千米)如下:
$+1,+3,-6,-1,-2,+5$.
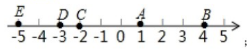
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,
E的位置.
(2)试求出该货车共行驶了多少千米.
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记
为负数,则运往A,B,C,D,E五个地点的水果重量可记为:$+50,-15,+25,-10,-15$.
该货车运送的水果总重量是多少千克?
一辆货车从仓库O出发在东西方向的街道上运送水果,规定向东为正方向,货车到达的5
个销售地点依次为A,B,C,D,E,最后回到仓库O,货车行驶的距离记录(单位:千米)如下:
$+1,+3,-6,-1,-2,+5$.
(1)请以仓库O为原点,向东为正方向,选择适当的单位长度,画出数轴,并标出A,B,C,D,
E的位置.
(2)试求出该货车共行驶了多少千米.
(3)如果货车运送的水果以100千克为标准重量,超过的千克数记为正数,不足的千克数记
为负数,则运往A,B,C,D,E五个地点的水果重量可记为:$+50,-15,+25,-10,-15$.
该货车运送的水果总重量是多少千克?
答案:
22.
(1)
(2)1 + 3 + |-6| + |-1| + |-2| + 5 = 18(千米)
答:共行驶了18千米.
(3)100×5 + 50 - 15 + 25 - 10 - 15 = 535(千克)
答:货车运送的水果总重量是535千克.
22.
(1)

(2)1 + 3 + |-6| + |-1| + |-2| + 5 = 18(千米)
答:共行驶了18千米.
(3)100×5 + 50 - 15 + 25 - 10 - 15 = 535(千克)
答:货车运送的水果总重量是535千克.
23.(本题满分12分)
如图,A,B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.
(1)请写出A,B中点M所对应的数.
(2)现有一点P从B点出发,以6单位/秒的速度向左运动,同时另一点Q恰好从A点出
发,以4单位/秒的速度向右运动.设点P,Q在数轴上的C点相遇,求C点对应的数.
(3)当点P从B点出发时,以6单位/秒的速度向左运动,同时另一点Q恰好从A点出发,
以4单位/秒的速度也向左运动.设点P,Q在数轴上的D点相遇,求D点对应的数.
如图,A,B分别为数轴上的两点,A点对应的数为-20,B点对应的数为100.

(1)请写出A,B中点M所对应的数.
(2)现有一点P从B点出发,以6单位/秒的速度向左运动,同时另一点Q恰好从A点出
发,以4单位/秒的速度向右运动.设点P,Q在数轴上的C点相遇,求C点对应的数.
(3)当点P从B点出发时,以6单位/秒的速度向左运动,同时另一点Q恰好从A点出发,
以4单位/秒的速度也向左运动.设点P,Q在数轴上的D点相遇,求D点对应的数.
答案:
23.
(1)M = $\frac{-20 + 100}{2}$ = 40
(2)设t秒后相遇.
6t + 4t = 120,
t = 12,
所以C = 100 - 6t = 28.
(3)设t秒后相遇.
4t + 120 = 6t,
t = 60,
所以D=100 - 6t = -260
(1)M = $\frac{-20 + 100}{2}$ = 40
(2)设t秒后相遇.
6t + 4t = 120,
t = 12,
所以C = 100 - 6t = 28.
(3)设t秒后相遇.
4t + 120 = 6t,
t = 60,
所以D=100 - 6t = -260
查看更多完整答案,请扫码查看


