第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
9. “区间测速”目前在全国大部分高速公路实行。所谓的“区间测速”,就是在两监测点安装监控和测速探头,测出同一辆车通过两个监测点的时间,如果这个平均车速超过了该路段的最高限速,即被判为超速。如图所示,监测点A、B相距30km,一辆轿车通过监测点A的速度为100km/h,通过监测点B的速度为110km/h,该路段最高限速为120km/h。
(1)“区间测速”的原理可以用公式
(2)原来检测的方法是监控探头判断通过监测点时的车速,如果按原来的方法,该轿车通过监测点A、B时
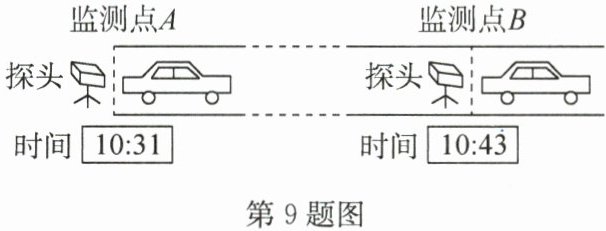
(1)“区间测速”的原理可以用公式
$v=\frac{s}{t}$
表示。(2)原来检测的方法是监控探头判断通过监测点时的车速,如果按原来的方法,该轿车通过监测点A、B时
不会
(选填“会”或“不会”)被判为超速。采用“区间测速”,这辆轿车从监测点A运动到B的平均速度是150
km/h,轿车会
(选填“会”或“不会”)被判为超速。
答案:
9.
(1)$v=\frac{s}{t}$
(2)不会 150 会
解析:
(1)“区间测速”是测出汽车通过固定路程的时间,根据$v=\frac{s}{t}$计算出汽车在通过这段路程时的平均速度来判断汽车是否超速,故测速原理可以用公式$v=\frac{s}{t}$表示。
(2)因为$v_{A}=100\ km/h<120\ km/h$,$v_{B}=110\ km/h<120\ km/h$,所以轿车不会被判为超速。由图可知,轿车的行驶时间$t = 12\ min = 0.2\ h$,则轿车的平均速度$v=\frac{s}{t}=\frac{30\ km}{0.2\ h}=150\ km/h>120\ km/h$,所以该轿车超速。
(1)$v=\frac{s}{t}$
(2)不会 150 会
解析:
(1)“区间测速”是测出汽车通过固定路程的时间,根据$v=\frac{s}{t}$计算出汽车在通过这段路程时的平均速度来判断汽车是否超速,故测速原理可以用公式$v=\frac{s}{t}$表示。
(2)因为$v_{A}=100\ km/h<120\ km/h$,$v_{B}=110\ km/h<120\ km/h$,所以轿车不会被判为超速。由图可知,轿车的行驶时间$t = 12\ min = 0.2\ h$,则轿车的平均速度$v=\frac{s}{t}=\frac{30\ km}{0.2\ h}=150\ km/h>120\ km/h$,所以该轿车超速。
10. 步行不仅是一种简易的健身运动,而且还能方便地对一些长度进行估测。
(1)人正常步行时,步距变化不大,因此,步距可作为身体上的一把“尺子”。为了使这把“尺子”更可靠,譬如用皮卷尺测出
(2)小冰测出自己的步距为0.6m,她从教学楼的一端走到另一端,共走了70步,则教学楼的长度是
(3)小冰按照上述的速度,从家到学校用时10min,则小冰的家到学校的路程是
(1)人正常步行时,步距变化不大,因此,步距可作为身体上的一把“尺子”。为了使这把“尺子”更可靠,譬如用皮卷尺测出
沿直线
(选填“走曲线”或“沿直线”)步行②10步或多步的距离,除以步数
(选填序号“①一步的距离”或“②10步或多步的距离,除以步数”),测出的步距误差较小。(2)小冰测出自己的步距为0.6m,她从教学楼的一端走到另一端,共走了70步,则教学楼的长度是
42
m,如果这个过程用时35s,则她步行的平均速度是1.2
m/s。(3)小冰按照上述的速度,从家到学校用时10min,则小冰的家到学校的路程是
720
m。
答案:
10.
(1)沿直线
(2)42 1.2
(3)720
解析:
(1)如果走曲线,则不易用皮卷尺测出通过的距离;如果只测量一步的距离作为步距,则误差较大。故为了使这把“尺子”更可靠,应用皮卷尺测出沿直线步行10步或多步的距离,再除以步数,此时测出的步距误差较小。
(2)小冰测出自己的步距为$0.6\ m$,她从教学楼的一端走到另一端,共走了70步,则教学楼的长度是$s = 0.6\ m × 70 = 42\ m$。如果这个过程用时35 s,则她步行的平均速度是$v=\frac{s}{t}=\frac{42\ m}{35\ s}=1.2\ m/s$。
(3)小冰按照上述的速度,从家到学校用时10 min,根据速度公式,则小冰的家到学校的路程是$s'=v t'=1.2\ m/s × 600\ s = 720\ m$。
(1)沿直线
(2)42 1.2
(3)720
解析:
(1)如果走曲线,则不易用皮卷尺测出通过的距离;如果只测量一步的距离作为步距,则误差较大。故为了使这把“尺子”更可靠,应用皮卷尺测出沿直线步行10步或多步的距离,再除以步数,此时测出的步距误差较小。
(2)小冰测出自己的步距为$0.6\ m$,她从教学楼的一端走到另一端,共走了70步,则教学楼的长度是$s = 0.6\ m × 70 = 42\ m$。如果这个过程用时35 s,则她步行的平均速度是$v=\frac{s}{t}=\frac{42\ m}{35\ s}=1.2\ m/s$。
(3)小冰按照上述的速度,从家到学校用时10 min,根据速度公式,则小冰的家到学校的路程是$s'=v t'=1.2\ m/s × 600\ s = 720\ m$。
11. 如图所示,滚尺是一种测量长度的工具,多用于跑道、事故、农业等道路测量。滚尺主要由计数器和滚轮组成,当滚轮沿着路径滚动时,通过记录的圈数可以得到路径的长度。小华想利用滚尺和手机秒表,测量自己步行的平均速度。
(1)将滚尺示数清零后,推动滚尺,手机同时计时,测出某次步行距离是13.8m,对应的时间为11.5s,则这段时间他步行的平均速度为
(2)已知该滚尺滚轮直径为D,用s表示滚尺测出的距离,则上述测量中轮子滚过的圈数$n=$
(3)长期使用后,滚轮的轮胎磨损严重,这将导致测量出的步行速度偏

(1)将滚尺示数清零后,推动滚尺,手机同时计时,测出某次步行距离是13.8m,对应的时间为11.5s,则这段时间他步行的平均速度为
$1.2\ m/s$
。(2)已知该滚尺滚轮直径为D,用s表示滚尺测出的距离,则上述测量中轮子滚过的圈数$n=$
$\frac{s}{\pi D}$
(用字母表示)。(3)长期使用后,滚轮的轮胎磨损严重,这将导致测量出的步行速度偏
大
。
答案:
11.
(1)$1.2\ m/s$
(2)$ \frac{s}{\pi D}$
(3)大 解析:
(1)小华的平均速度$v=\frac{s}{t}=\frac{13.8\ m}{11.5\ s}=1.2\ m/s$。
(2)该滚轮一周的长度$L = \pi D$,轮子滚过的圈数$n=\frac{s}{L}=\frac{s}{\pi D}$。
(3)当滚轮的轮胎磨损严重时,计数器上显示的距离比实际距离大,而测量时间准确,根据$v=\frac{s}{t}$可知,测出的步行速度偏大。
(1)$1.2\ m/s$
(2)$ \frac{s}{\pi D}$
(3)大 解析:
(1)小华的平均速度$v=\frac{s}{t}=\frac{13.8\ m}{11.5\ s}=1.2\ m/s$。
(2)该滚轮一周的长度$L = \pi D$,轮子滚过的圈数$n=\frac{s}{L}=\frac{s}{\pi D}$。
(3)当滚轮的轮胎磨损严重时,计数器上显示的距离比实际距离大,而测量时间准确,根据$v=\frac{s}{t}$可知,测出的步行速度偏大。
12. 小昊是地地道道的“魔方迷”,家里有各种各样的魔方,如图甲、乙和丙所示。学习物理知识后,善于思考的小昊想借助于刻度尺和秒表来测量圆柱形魔方丙滚上斜面的平均速度,于是小昊找来了两个大小和形状均相同的正方体魔方甲和乙,借助于两块相同的长木板搭建了两个斜面,如图丁所示,并做了如下探究实验。
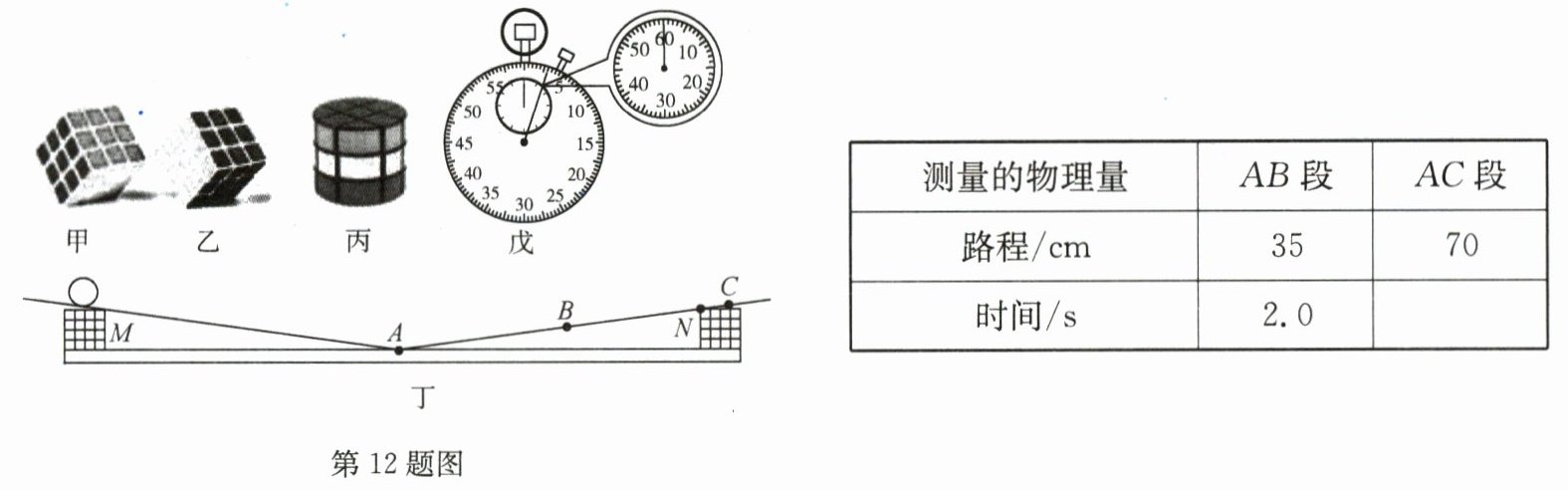
(1)开始实验后,他将魔方丙从左侧斜面的最高位置由静止开始释放使其滚下,可是发现魔方每次从右侧斜面底端滚上去的时间都比较短,不容易测量。为了更准确地测量时间,小昊应该适当地使
(2)改进装置后小昊重新实验,上表是小昊的部分实验数据,测量AC段时间后发现秒表显
(3)由实验数据可知:魔方在AB段的平均速度为

(1)开始实验后,他将魔方丙从左侧斜面的最高位置由静止开始释放使其滚下,可是发现魔方每次从右侧斜面底端滚上去的时间都比较短,不容易测量。为了更准确地测量时间,小昊应该适当地使
左侧
(选填“左侧”或“右侧”)斜面变缓。(2)改进装置后小昊重新实验,上表是小昊的部分实验数据,测量AC段时间后发现秒表显
示
的
示数为8s,突然想起了测量前忘记将秒表调零,若测量前秒表的示数如图戊所示,则魔方在AC段滚动的真实时间为5
s。(3)由实验数据可知:魔方在AB段的平均速度为
17.5
cm/s;通过计算可知魔方在AB段的平均速度大于
(选填“大于”“小于”或“等于”)在BC段的平均速度;魔方丙从斜面底端滚动到斜面顶端的运动是减速
(选填“加速”“减速”或“匀速”)运动。
答案:
12.
(1)左侧
(2)5
(3)17.5 大于 减速
解析:
(1)为了更准确地测量时间,小昊应该适当地使左侧的斜面减缓些,就会延长魔方滚上右侧斜面的时间,便于测量时间。
(2)秒表示数为$3\ s$,则魔方在$AC$段滚动的真实时间为$t = 8\ s - 3\ s = 5\ s$。
(3)魔方在$AB$段的平均速度为$v_{AB}=\frac{s_{AB}}{t_{AB}}=\frac{35\ cm}{2.0\ s}=17.5\ cm/s$,在$BC$段的平均速度为$v_{BC}=\frac{s_{BC}}{t_{BC}}=\frac{70\ cm - 35\ cm}{5\ s - 2.0\ s}=11.67\ cm/s$,故魔方在$AB$段的平均速度大于在$BC$段的平均速度,魔方丙从斜面底端滚动到斜面顶端时,速度慢慢减小,故其做减速运动。
(1)左侧
(2)5
(3)17.5 大于 减速
解析:
(1)为了更准确地测量时间,小昊应该适当地使左侧的斜面减缓些,就会延长魔方滚上右侧斜面的时间,便于测量时间。
(2)秒表示数为$3\ s$,则魔方在$AC$段滚动的真实时间为$t = 8\ s - 3\ s = 5\ s$。
(3)魔方在$AB$段的平均速度为$v_{AB}=\frac{s_{AB}}{t_{AB}}=\frac{35\ cm}{2.0\ s}=17.5\ cm/s$,在$BC$段的平均速度为$v_{BC}=\frac{s_{BC}}{t_{BC}}=\frac{70\ cm - 35\ cm}{5\ s - 2.0\ s}=11.67\ cm/s$,故魔方在$AB$段的平均速度大于在$BC$段的平均速度,魔方丙从斜面底端滚动到斜面顶端时,速度慢慢减小,故其做减速运动。
查看更多完整答案,请扫码查看


