《2025年自主学习指导课程与测试八年级物理上册沪科版》

17. 小明同学到钢铁厂参加社会实践活动,师傅教他加工零件,他很想知道这个质地均匀的零件是什么材料做成的,于是把它带回学校利用天平和量筒来测这个零件的密度。具体操作如图 9:

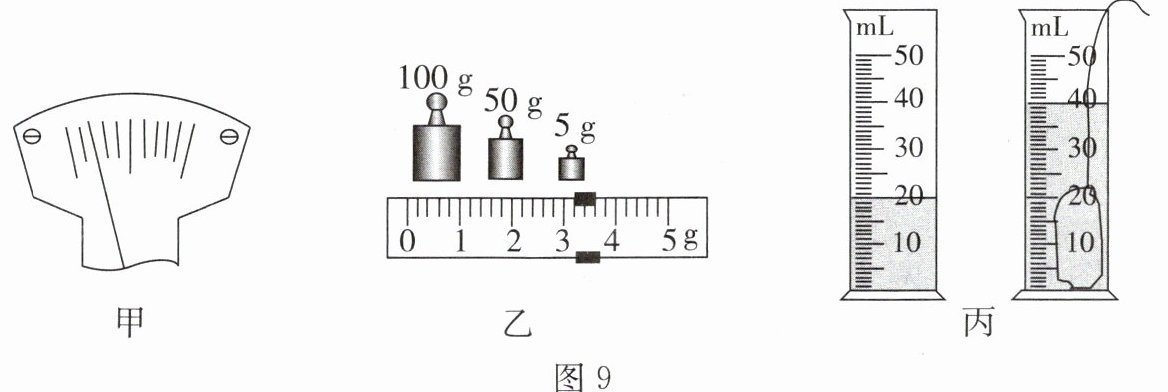
(1) 把天平放在水平台上,并将游码移至标尺左端零刻度线处;调节天平横梁平衡,发现指针在分度盘标尺上的位置如图 9 甲所示,此时应将平衡螺母向右(选填“左”或“右”)调节。
(2) 用调节好的天平测零件的质量,天平平衡时,砝码的质量及游码在标尺上的位置如图 9 乙所示,则零件的质量为158.2$g$,用量筒测得零件的体积如图 9 丙所示,零件的体积为20$cm^3$,由此可算得金属零件的密度为7.91$g/cm^3$。
(3) 该零件磨损后,它的密度将不变(选填“变大”“变小”或“不变”)。

答案：
(1)右
(2)158.2 20 7.91
(3)不变

18. 体积是 $40\ cm^3$ 的铝球,它的质量是 $67.5\ g$,这个铝球是空心的还是实心的?若空心,请计算出空心部分体积。$(\rho_{铝}= 2.7×10^{3}\ kg/m^3)$

答案： 解：已知$\rho_{铝}=2.7×10^{3}kg/m^{3}=2.7g/cm^{3}$，$m = 67.5g$。
根据密度公式$\rho=\frac{m}{V}$，可得铝球中铝的体积$V_{铝}=\frac{m}{\rho_{铝}}=\frac{67.5g}{2.7g/cm^{3}} = 25cm^{3}$。
因为$V_{球}=40cm^{3}$，$V_{铝}=25cm^{3}$，$V_{球}＞V_{铝}$，所以这个铝球是空心的。
空心部分体积$V_{空}=V_{球}-V_{铝}=40cm^{3}-25cm^{3}=15cm^{3}$。
综上，这个铝球是空心的，空心部分体积为$15cm^{3}$。

19. 有一油罐车,灌装了 $20\ m^3$ 的石油,该车在高速某水平路段沿直线匀速行驶 $2400\ m$ 耗时 $2\ min$。为了估算油罐车所装石油的质量,从中取出了 $30\ cm^3$ 石油,称得质量为 $24.6\ g$。求:
(1) 油罐车行驶的平均速度;
(2) 油罐车所装石油的密度;
(3) 油罐车所装石油的质量。

答案： 1. （1）解：
已知$s = 2400m$，$t = 2min=2×60s = 120s$。
根据速度公式$v=\frac{s}{t}$，可得$v=\frac{2400m}{120s}=20m/s$。
2. （2）解：
已知$m = 24.6g$，$V = 30cm^{3}$。
根据密度公式$\rho=\frac{m}{V}$，可得$\rho=\frac{24.6g}{30cm^{3}} = 0.82g/cm^{3}=0.82×10^{3}kg/m^{3}$。
3. （3）解：
已知$V_{总}=20m^{3}$，$\rho = 0.82×10^{3}kg/m^{3}$。
根据质量公式$m=\rho V$，可得$m_{总}=\rho V_{总}=0.82×10^{3}kg/m^{3}×20m^{3}=1.64×10^{4}kg$。
综上，答案依次为：（1）$20m/s$；（2）$0.82×10^{3}kg/m^{3}$；（3）$1.64×10^{4}kg$。