第5页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
若菱形的两条对角线的长分别是$a$,$b$,则菱形的面积等于
$\frac{1}{2}ab$
。
答案:
$\frac{1}{2}ab$
1. 下列关于某个四边形的三个结论:①对角线互相平分;②是一个菱形;③是一个平行四边形。下列推理过程正确的是(
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
A
)A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
答案:
1. A
2. 如图,在菱形ABCD中,E,F,G,H分别是菱形四边的中点,连接EG,FH,且EG,FH交于点O,则图中共有菱形(
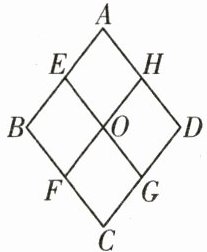
A.$4$个
B.$5$个
C.$6$个
D.$7$个
B
)
A.$4$个
B.$5$个
C.$6$个
D.$7$个
答案:
2. B
3. 若菱形的两条对角线长分别是$16\ cm和12\ cm$,则它的边长为
10 cm
,面积为96 cm²
。
答案:
3. 10 cm 96 cm²
4. 如图,菱形$ABCD的对角线的长分别为2和5$,$P是对角线AC$上任意一点(点$P不与点A$,$C$重合),且$PE// BC交AB于点E$,$PF// CD交AD于点F$,则阴影部分的面积是
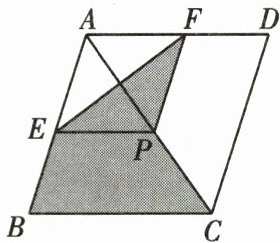
2.5
。
答案:
4. 2.5
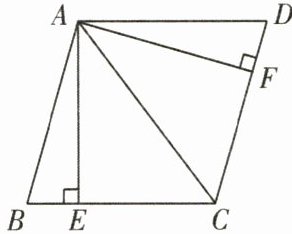
5. 如图,在$□ ABCD$中,$AE\perp BC$,$AF\perp CD$,垂足分别为$E$,$F$,且$BE = DF$。
(1)求证:$□ ABCD$是菱形;
(2)若$AB = 5$,$AC = 6$,求$□ ABCD$的面积。
(1)求证:$□ ABCD$是菱形;
(2)若$AB = 5$,$AC = 6$,求$□ ABCD$的面积。

答案:
5.
(1)证明:
∵四边形 ABCD 是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°.
∵BE=DF,
∴△AEB≌△AFD(SAS).
∴AB=AD,
∴四边形 ABCD 是菱形.
(2)解:连接 BD 交 AC 于点 O.
∵四边形 ABCD 是菱形,AC=6,
∴AC⊥BD,
AO=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
∵AB=5,AO=3,

∴BO=$\sqrt{AB^2 - AO^2}$=$\sqrt{5^2 - 3^2}$=4,
∴BD=2BO=8,
∴S${}_{平行四边形ABCD}$=$\frac{1}{2}$×AC×BD=24.
5.
(1)证明:
∵四边形 ABCD 是平行四边形,
∴∠B=∠D.
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°.
∵BE=DF,
∴△AEB≌△AFD(SAS).
∴AB=AD,
∴四边形 ABCD 是菱形.
(2)解:连接 BD 交 AC 于点 O.
∵四边形 ABCD 是菱形,AC=6,
∴AC⊥BD,
AO=OC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
∵AB=5,AO=3,

∴BO=$\sqrt{AB^2 - AO^2}$=$\sqrt{5^2 - 3^2}$=4,
∴BD=2BO=8,
∴S${}_{平行四边形ABCD}$=$\frac{1}{2}$×AC×BD=24.
1. 如图,$O既是AB$的中点,又是$CD$的中点,并且$AB\perp CD$,连接$AC$,$BC$,$AD$,$BD$,则这四条线段的大小关系是(
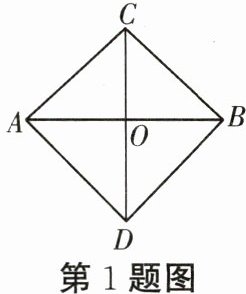
A.全相等
B.互不相等
C.只有两条相等
D.不能确定
A
)
A.全相等
B.互不相等
C.只有两条相等
D.不能确定
答案:
1. A
2. 如图,将两根宽度都为$1$的纸条叠放在一起,如果$\angle DAB = 45^{\circ}$,则四边形$ABCD$的面积为(
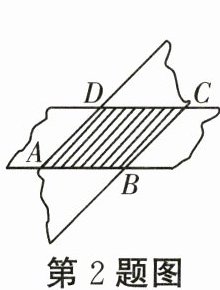
A.$1$
B.$\frac{1}{2}$
C.$\sqrt{2}$
D.$\frac{\sqrt{2}}{2}$
C
)
A.$1$
B.$\frac{1}{2}$
C.$\sqrt{2}$
D.$\frac{\sqrt{2}}{2}$
答案:
2. C
3. 如图,①以点$A$为圆心,半径为$2\ cm$画弧,分别交$\angle MAN的两边AM$,$AN于点B$,$D$;②以点$B$为圆心,$AD$长为半径画弧,再以点$D$为圆心,$AB$长为半径画弧,两弧交于点$C$;③分别连接$BC$,$CD$,$AC$。若$\angle MAN = 60^{\circ}$,则$\angle ACB$的大小为
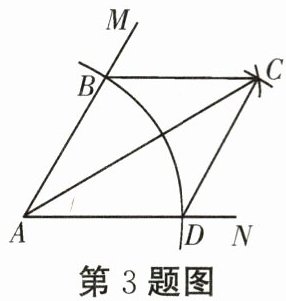
30°
。
答案:
3. 30°
查看更多完整答案,请扫码查看


