《2025年同步精练广东九年级数学上册北师大版》

1. 有一个面积为$16 cm^2$的梯形,它的一条底边长为3 cm,另一条底边长比它的高长1 cm,若设这条底边长为x cm,根据题意,列出方程整理后得(A)
A.$x^2 + 2x - 35 = 0$
B.$x^2 + 2x - 70 = 0$
C.$x^2 - 2x - 35 = 0$
D.$x^2 - 2x - 70 = 0$

答案： A

2. 若直角三角形的三边长是三个连续偶数,则这个直角三角形的面积是(B)
A.12
B.24
C.30
D.40

答案： B

3. 将一块正方形铁皮的四角各剪去一个边长为3 cm的小正方形,做成一个无盖的盒子,已知盒子的容积是$300 cm^3,$则原铁皮的边长为(D)
A.10 cm
B.13 cm
C.14 cm
D.16 cm

答案： D

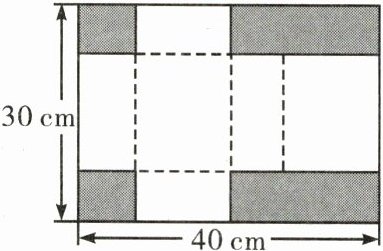
4. 如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即为剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计)。若长方形纸板边长分别为40 cm和30 cm,且折成的长方体盒子表面积是$888 cm^2,$则剪掉的小正方形的边长为6cm。

答案： 6

5. 有一张长40 cm、宽30 cm的桌面,桌面正中间铺有一块垫布,垫布的面积是桌面面积的$\frac{1}{2}$,且桌面四边露出部分宽度相同,若设四周宽度为x cm,则所列一元二次方程是(40-2x)(30-2x)=$\frac{1}{2}$×40×30。

答案： (40-2x)(30-2x)=$\frac{1}{2}$×40×30

6. 如图,邻边不等的矩形花圃ABCD,它的一边AD是利用已有的围墙,另外三边围的栅栏的总长度是6 m.若矩形的面积为$4 m^2,$求AB的长.(可利用的围墙长度超过6 m)

答案： AB的长为1 m.

7. 如图,要利用一面墙(墙长为25 m)建牛圈,用100 m的围栏围成总面积为$400 m^2$的三个大小相同的矩形牛圈,求矩形牛圈AB,BC的长。

答案： 解:设AB=x m,则BC=(100-4x)m,
依题意得x(100-4x)=400,解得x₁=20,x₂=5,
当x=20时,BC=100-4x=20＜25,符合题意;
当x=5时,BC=100-4x=80＞25,不符合题意,舍去.
答:牛圈AB的长为20 m,BC的长为20 m.

8. 如图,在△ABC中,∠C = 90°,BC = 5 cm,AC = 7 cm.两个动点P,Q分别从B,C两点同时出发,其中点P以1 cm/s的速度沿着线段BC向点C运动,点Q以2 cm/s的速度沿着线段CA向点A运动.
(1)P,Q两点在运动过程中,经过几秒△PCQ的面积等于$4 cm^2？$经过几秒PQ的长度等于5 cm？
(2)P,Q两点在运动过程中,四边形ABPQ的面积能否等于$11 cm^2？$试说明理由。

答案：
(1)设经过x s,△PCQ的面积为4 cm²,即
$\frac{1}{2}$×(5-x)×2x=4,解得x₁=1,x₂=4(不合题意,舍去).
∴经过1 s,△PCQ的面积等于4 cm².
设经过t s PQ的长度等于5 cm.
∵PC²+CQ²=PQ²,PC=5-t,CQ=2t,PQ=5,
∴(5-t)²+(2t)²=5²,解得t₁=0,t₂=2.
∴经过0s或2s,PQ的长度等于5 cm.
(2)若P,Q两点在运动过程中,四边形ABPQ的面积能等于11 cm²,即S△PCQ=$\frac{5×7}{2}$-11=$\frac{13}{2}$,即$\frac{1}{2}$×(5-t)×2t=$\frac{13}{2}$,
化简,得2t²-10t+13=0.
∵Δ=b²-4ac=10×10-4×2×13＜0,
∴此方程无解.
∴四边形ABPQ的面积不能等于11 cm².

9. 收发电子红包已成为人们进行交流、增进感情的一种方式,下面是甜甜和她的妹妹在春节期间的对话。

(1)2018年到2020年甜甜和她妹妹在春节收到红包的年增长率是多少？
(2)2020年春节甜甜和她妹妹各收到了多少钱的电子红包？
（1）设年增长率为$x$：根据公式$a(1 + x)^{n}=b$（$a$为初始值，$x$为增长率，$n$为增长次数，$b$为最终值），这里$a = 400$，$n = 2$，$b = 484$，则$400(1 + x)^{2}=484$。化简方程：两边同时除以$400$得$(1 + x)^{2}=\frac{484}{400}$，即$(1 + x)^{2}=1.21$。开平方得$1 + x=\pm1.1$。当$1 + x = 1.1$时，$x = 0.1=10\%$；当$1 + x=-1.1$时，$x=-2.1$（增长率不能为负，舍去）。所以年增长率是$10\%$。
（2）设2020年春节甜甜收到$y$元电子红包，则妹妹收到$(2y + 34)$元：根据2020年共收到$484$元，可列方程$y+(2y + 34)=484$。解方程：去括号得$y+2y + 34 = 484$。移项得$y+2y=484 - 34$。合并同类项得$3y=450$。两边同时除以$3$得$y = 150$。则妹妹收到的钱数为：$2y+34=2×150 + 34=300 + 34 = 334$（元）。所以2020年春节甜甜收到$150$元，妹妹收到$334$元。

答案： 1. （1）设年增长率为$x$：
根据公式$a(1 + x)^{n}=b$（$a$为初始值，$x$为增长率，$n$为增长次数，$b$为最终值），这里$a = 400$，$n = 2$，$b = 484$，则$400(1 + x)^{2}=484$。
化简方程：
两边同时除以$400$得$(1 + x)^{2}=\frac{484}{400}$，即$(1 + x)^{2}=1.21$。
开平方得$1 + x=\pm1.1$。
当$1 + x = 1.1$时，$x = 0.1=10\%$；当$1 + x=-1.1$时，$x=-2.1$（增长率不能为负，舍去）。
2. （2）设2020年春节甜甜收到$y$元电子红包，则妹妹收到$(2y + 34)$元：
根据2020年共收到$484$元，可列方程$y+(2y + 34)=484$。
解方程：
去括号得$y+2y + 34 = 484$。
移项得$y+2y=484 - 34$。
合并同类项得$3y=450$。
两边同时除以$3$得$y = 150$。
则妹妹收到的钱数为：$2y+34=2×150 + 34=300 + 34 = 334$（元）。
综上，（1）年增长率是$10\%$；（2）2020年春节甜甜收到$150$元，妹妹收到$334$元。