第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4. 如图,在正方形ABCD中,F是CD上的一点,BF与AC交于点E.若∠CBF= 20°,则∠AED=
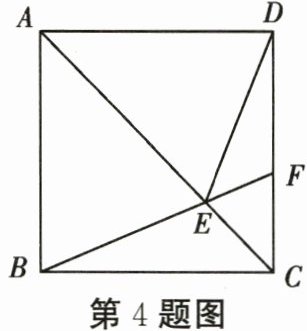
65°
.
答案:
$65^{\circ }$
5. 如图,P为边长为1的正方形ABCD内的一点,△PAB为等边三角形,则$S_{△ADP}+S_{△BPC}$=
]
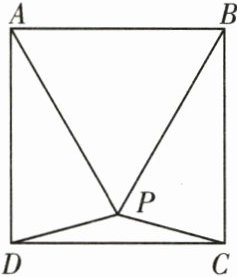
0.5
.]

答案:
0.5
6. 如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的平分线分别交AB,BD于M,N两点,若$BM= \sqrt{2}$,则正方形ABCD的边长为
]
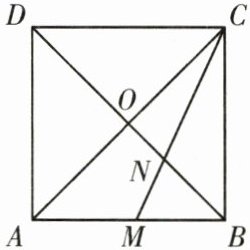
$2+\sqrt {2}$
.]

答案:
$2+\sqrt {2}$
7. 如图,已知在正方形ABCD中,E是边CD上的一点,F为BC延长线上的一点,CE= CF.
(1)求证:△BCE≌△DCF;
(2)若∠BEC= 60°,求∠EFD的度数.
]

(1)求证:△BCE≌△DCF;
(2)若∠BEC= 60°,求∠EFD的度数.
]

答案:
(1)证明:
∵四边形ABCD是正方形,$\therefore BC=DC,\angle BCD=90^{\circ }.$
在$\triangle BCE$和$\triangle DCF$中,
$BC=DC,\angle BCE=\angle DCF=90^{\circ },CE=CF,$
$\therefore \triangle BCE\cong \triangle DCF(SAS).$
(2)解:$\angle EFD=15^{\circ }.$
(1)证明:
∵四边形ABCD是正方形,$\therefore BC=DC,\angle BCD=90^{\circ }.$
在$\triangle BCE$和$\triangle DCF$中,
$BC=DC,\angle BCE=\angle DCF=90^{\circ },CE=CF,$
$\therefore \triangle BCE\cong \triangle DCF(SAS).$
(2)解:$\angle EFD=15^{\circ }.$
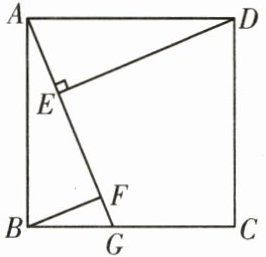
8. (2020·呼和浩特)如图,正方形ABCD,G是BC边上任意一点(不与点B,C重合),DE⊥AG于点E,BF//DE,且交AG于点F.
(1)求证:AF-BF= EF;
(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置;如不可能,请说明理由.
]
(1)求证:AF-BF= EF;
(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置;如不可能,请说明理由.
]

答案:
(1)证明:
∵四边形ABCD是正方形,
$\therefore AB=AD,\angle BAF+\angle DAE=90^{\circ }.$
$\because DE\perp AG,\therefore \angle DAE+\angle ADE=90^{\circ },\therefore \angle ADE=\angle BAF.$
又$\because BF// DE,\therefore \angle BFA=\angle AED=90^{\circ },$
$\therefore \triangle ABF\cong \triangle DAE(AAS),\therefore AE=BF,$
$\therefore AF - BF=AF - AE=EF.$
(2)解:不可能.理由如下:
如图,若要四边形BFDE是平行四边形,
已知$DE// BF$,则当$DE=BF$时,四边形BFDE为平行四边形,
$\because DE=AF,\therefore BF=AF$,即此时$\angle BAF=45^{\circ },$
而点G不与点C重合,
$\therefore \angle BAF\neq 45^{\circ }$,矛盾,
∴四边形BFDE不可能是平行四边形.

(1)证明:
∵四边形ABCD是正方形,
$\therefore AB=AD,\angle BAF+\angle DAE=90^{\circ }.$
$\because DE\perp AG,\therefore \angle DAE+\angle ADE=90^{\circ },\therefore \angle ADE=\angle BAF.$
又$\because BF// DE,\therefore \angle BFA=\angle AED=90^{\circ },$
$\therefore \triangle ABF\cong \triangle DAE(AAS),\therefore AE=BF,$
$\therefore AF - BF=AF - AE=EF.$
(2)解:不可能.理由如下:
如图,若要四边形BFDE是平行四边形,
已知$DE// BF$,则当$DE=BF$时,四边形BFDE为平行四边形,
$\because DE=AF,\therefore BF=AF$,即此时$\angle BAF=45^{\circ },$
而点G不与点C重合,
$\therefore \angle BAF\neq 45^{\circ }$,矛盾,
∴四边形BFDE不可能是平行四边形.

9. 如图①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA= PE,PE交CD于点F.
(1)求证:PC= PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC= 120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
]
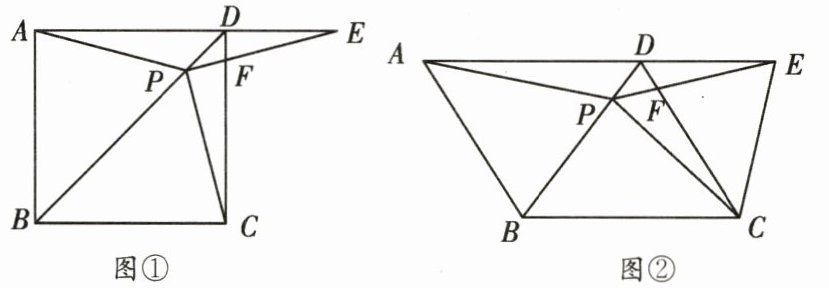
(1)求证:PC= PE;
(2)求∠CPE的度数;
(3)如图②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC= 120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
]

答案:
(1)证明:在正方形ABCD中,$AB=BC,\angle ABP=\angle CBP=45^{\circ },$
在$\triangle ABP$和$\triangle CBP$中,
$AB=BC,\angle ABP=\angle CBP,PB=PB,$
$\therefore \triangle ABP\cong \triangle CBP(SAS).\therefore PA=PC,$
$\because PA=PE,\therefore PC=PE.$
(2)解:由
(1)知$\triangle ABP\cong \triangle CBP,$
$\therefore \angle BAP=\angle BCP,\therefore \angle DAP=\angle DCP.$
$\because PA=PE,\therefore \angle DAP=\angle E,\therefore \angle DCP=\angle E.$
$\because \angle CFP=\angle EFD$(对顶角相等),
$\therefore 180^{\circ }-\angle PFC-\angle PCF=180^{\circ }-\angle DFE-\angle E,$
即$\angle CPE=\angle EDF=90^{\circ }.$
(3)在菱形ABCD中,$AB=BC,\angle ABP=\angle CBP=60^{\circ },$
在$\triangle ABP$和$\triangle CBP$中,
$AB=BC,\angle ABP=\angle CBP,PB=PB,$
$\therefore \triangle ABP\cong \triangle CBP(SAS),\therefore PA=PC,\angle BAP=\angle BCP.$
$\because PA=PE,\therefore PC=PE,\therefore \angle DAP=\angle DCP,$
$\because PA=PC,\therefore \angle DAP=\angle AEP,\therefore \angle DCP=\angle AEP,$
$\because \angle CFP=\angle EFD$(对顶角相等),
$\therefore 180^{\circ }-\angle PFC-\angle PCF=180^{\circ }-\angle DFE-\angle AEP,$
即$\angle CPF=\angle EDF=180^{\circ }-\angle ADC=180^{\circ }-120^{\circ }=60^{\circ },$
$\therefore \triangle EPC$是等边三角形,$\therefore PC=CE,\therefore AP=CE.$
(1)证明:在正方形ABCD中,$AB=BC,\angle ABP=\angle CBP=45^{\circ },$
在$\triangle ABP$和$\triangle CBP$中,
$AB=BC,\angle ABP=\angle CBP,PB=PB,$
$\therefore \triangle ABP\cong \triangle CBP(SAS).\therefore PA=PC,$
$\because PA=PE,\therefore PC=PE.$
(2)解:由
(1)知$\triangle ABP\cong \triangle CBP,$
$\therefore \angle BAP=\angle BCP,\therefore \angle DAP=\angle DCP.$
$\because PA=PE,\therefore \angle DAP=\angle E,\therefore \angle DCP=\angle E.$
$\because \angle CFP=\angle EFD$(对顶角相等),
$\therefore 180^{\circ }-\angle PFC-\angle PCF=180^{\circ }-\angle DFE-\angle E,$
即$\angle CPE=\angle EDF=90^{\circ }.$
(3)在菱形ABCD中,$AB=BC,\angle ABP=\angle CBP=60^{\circ },$
在$\triangle ABP$和$\triangle CBP$中,
$AB=BC,\angle ABP=\angle CBP,PB=PB,$
$\therefore \triangle ABP\cong \triangle CBP(SAS),\therefore PA=PC,\angle BAP=\angle BCP.$
$\because PA=PE,\therefore PC=PE,\therefore \angle DAP=\angle DCP,$
$\because PA=PC,\therefore \angle DAP=\angle AEP,\therefore \angle DCP=\angle AEP,$
$\because \angle CFP=\angle EFD$(对顶角相等),
$\therefore 180^{\circ }-\angle PFC-\angle PCF=180^{\circ }-\angle DFE-\angle AEP,$
即$\angle CPF=\angle EDF=180^{\circ }-\angle ADC=180^{\circ }-120^{\circ }=60^{\circ },$
$\therefore \triangle EPC$是等边三角形,$\therefore PC=CE,\therefore AP=CE.$
查看更多完整答案,请扫码查看


