第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
6. 下列随机事件的概率:
①同时抛掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率;
②某作物的种子在一定条件下的发芽率;
③抛一枚图钉,“钉尖向下”的概率;
④投掷一枚均匀的骰子,朝上一面为偶数的概率。
既可以用列举法求得,又可以用频率估计获得的是
①同时抛掷两枚质地均匀的硬币,两枚硬币全部正面朝上的概率;
②某作物的种子在一定条件下的发芽率;
③抛一枚图钉,“钉尖向下”的概率;
④投掷一枚均匀的骰子,朝上一面为偶数的概率。
既可以用列举法求得,又可以用频率估计获得的是
①④
。(填序号)
答案:
①④
7. 有$400$名同学,其中一定至少有$2$人的生日相同吗?若有$367$名同学呢?说说你的理由。
答案:
400位同学中一定有2个人的生日相同,367位同学中也一定有2个人的生日相同.
8. 开学前,小明去商场买书包,商场在搞促销活动,买$1个书包可以送2支笔和1$本书。
(1)若有$3$支不同的笔可供选择,其中黑色$2$支,红色$1$支,试用树状图表示小明依次抽取$2$支笔的所有可能的情况,并求出抽取的$2$支笔均是黑色的概率;
(2)若有$6$本不同的书可供选择,要在其中抽$1$本,请你帮助小明设计一种用替代物模拟抽书的方法。
(1)若有$3$支不同的笔可供选择,其中黑色$2$支,红色$1$支,试用树状图表示小明依次抽取$2$支笔的所有可能的情况,并求出抽取的$2$支笔均是黑色的概率;
(2)若有$6$本不同的书可供选择,要在其中抽$1$本,请你帮助小明设计一种用替代物模拟抽书的方法。
答案:
(1)分别用$A_1$,$A_2$表示2支黑色笔,B表示红色笔.从3支笔中抽取2支笔的结果用树状图表示如图.从图中看出,一共有6种等可能的结果,其中2支笔是黑色的结果有2种.所以P(抽取的2支笔均是黑色)=$\frac{2}{6}$=$\frac{1}{3}$.
(2)方法不唯一,如:用6张不同的扑克牌分别代表6本不同的书,则从6张扑克牌中抽到某一张扑克牌就相当于抽到某一本书;或者用普通的正方体骰子投掷1次,掷得的点数1,2,3,4,5,6分别代表6本不同的书,则掷得某一个点数就相当于抽到某一本书.
(1)分别用$A_1$,$A_2$表示2支黑色笔,B表示红色笔.从3支笔中抽取2支笔的结果用树状图表示如图.从图中看出,一共有6种等可能的结果,其中2支笔是黑色的结果有2种.所以P(抽取的2支笔均是黑色)=$\frac{2}{6}$=$\frac{1}{3}$.
(2)方法不唯一,如:用6张不同的扑克牌分别代表6本不同的书,则从6张扑克牌中抽到某一张扑克牌就相当于抽到某一本书;或者用普通的正方体骰子投掷1次,掷得的点数1,2,3,4,5,6分别代表6本不同的书,则掷得某一个点数就相当于抽到某一本书.
9. “中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,某校开展了以“梦想中国,逐梦前行”为主题的摄影大赛,要求参赛学生每人交一件作品,现将参赛的$50$件作品的成绩进行统计如下:
(单位:分)
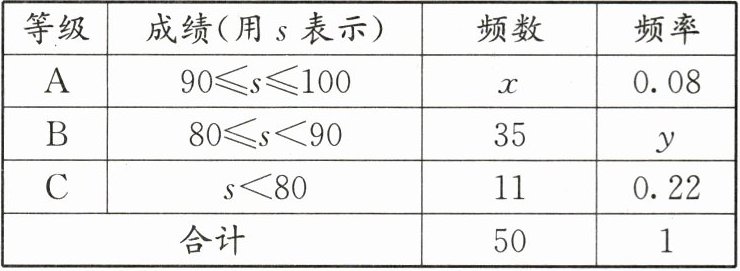
请根据上表提供的信息,解答下列问题:
(1)表中$x$的值为
(2)将本次参赛作品获得$A等级的学生依次用A_1$,$A_2$,$A_3$,…表示,现该校决定从本次参赛作品获得$A$等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用画树状图法或列表法求恰好抽到学生$A_1和A_2$的概率。
(单位:分)

请根据上表提供的信息,解答下列问题:
(1)表中$x$的值为
4
,$y$的值为______0.7
;(2)将本次参赛作品获得$A等级的学生依次用A_1$,$A_2$,$A_3$,…表示,现该校决定从本次参赛作品获得$A$等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用画树状图法或列表法求恰好抽到学生$A_1和A_2$的概率。
答案:
1. (1)
根据频率公式$频率=\frac{频数}{总数}$,已知总数$n = 50$,$A$等级频率$f_{A}=0.08$。
由$x = n× f_{A}$,可得$x=50×0.08 = 4$。
又因为$y=\frac{35}{50}=0.7$。
所以$x$的值为$4$,$y$的值为$0.7$。
2. (2)
$A$等级学生有$x = 4$人,即$A_1$,$A_2$,$A_3$,$A_4$。
列表法:
列表如下:
| | $A_1$ | $A_2$ | $A_3$ | $A_4$ |
| --- | --- | --- | --- | --- |
| $A_1$ | - | $(A_1,A_2)$ | $(A_1,A_3)$ | $(A_1,A_4)$ |
| $A_2$ | $(A_2,A_1)$ | - | $(A_2,A_3)$ | $(A_2,A_4)$ |
| $A_3$ | $(A_3,A_1)$ | $(A_3,A_2)$ | - | $(A_3,A_4)$ |
| $A_4$ | $(A_4,A_1)$ | $(A_4,A_2)$ | $(A_4,A_3)$ | - |
从表中可以看出,一共有$n = 12$种等可能的结果,其中恰好抽到$A_1$和$A_2$的结果有$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
综上,(1)$x = 4$,$y = 0.7$;(2)恰好抽到学生$A_1$和$A_2$的概率为$\frac{1}{6}$。
根据频率公式$频率=\frac{频数}{总数}$,已知总数$n = 50$,$A$等级频率$f_{A}=0.08$。
由$x = n× f_{A}$,可得$x=50×0.08 = 4$。
又因为$y=\frac{35}{50}=0.7$。
所以$x$的值为$4$,$y$的值为$0.7$。
2. (2)
$A$等级学生有$x = 4$人,即$A_1$,$A_2$,$A_3$,$A_4$。
列表法:
列表如下:
| | $A_1$ | $A_2$ | $A_3$ | $A_4$ |
| --- | --- | --- | --- | --- |
| $A_1$ | - | $(A_1,A_2)$ | $(A_1,A_3)$ | $(A_1,A_4)$ |
| $A_2$ | $(A_2,A_1)$ | - | $(A_2,A_3)$ | $(A_2,A_4)$ |
| $A_3$ | $(A_3,A_1)$ | $(A_3,A_2)$ | - | $(A_3,A_4)$ |
| $A_4$ | $(A_4,A_1)$ | $(A_4,A_2)$ | $(A_4,A_3)$ | - |
从表中可以看出,一共有$n = 12$种等可能的结果,其中恰好抽到$A_1$和$A_2$的结果有$m = 2$种。
根据概率公式$P=\frac{m}{n}$,可得$P=\frac{2}{12}=\frac{1}{6}$。
综上,(1)$x = 4$,$y = 0.7$;(2)恰好抽到学生$A_1$和$A_2$的概率为$\frac{1}{6}$。
查看更多完整答案,请扫码查看


