《2025年课课练九年级物理上册苏科版》

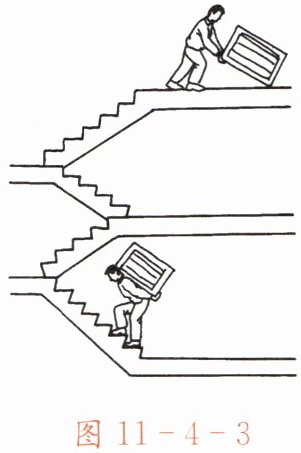
学校买了一箱物理器材,王老师将它从一楼搬运到三楼(图 11-4-3)。小丽想测量王老师搬运器材过程中对箱子做功的功率。
(1)测量所需要的器材有：磅秤、刻度尺、秒表。
(2)小丽设计的测量步骤如下,其中多余的步骤是b(填字母)。
a. 测出箱子所受的重力
b. 测出楼梯的总长度
c. 测出一楼到三楼的竖直高度
d. 测出王老师上楼梯所用的时间
e. 算出王老师搬运箱子的功率
(3)请你帮小丽设计一个实验记录表格。

答案： （1）磅秤、刻度尺、秒表 （2）b （3）表格如下：
箱子的质量
m/kg
箱子所受的
重力G/N
一楼到三楼的
竖直高度h/m
王老师上楼梯所用的
时间t/s
王老师搬运箱子的
功率P/W

1. 人类在各种活动中,需要将重物移动到某一位置以实现一定的目的,为实现目的而对重物做的功叫作有用功。在使用机械后,人们通过对机械做功来实现目的,这就需要克服机械的重力和摩擦等做一些人们并不需要而又不得不做的功,叫作额外功。人们利用机械所做的功,包括通过机械对重物做的功和克服机械自重及摩擦所做的功,叫作总功。用公式表示上述三个功的关系为$W_{总}=W_{有}+W_{额}$。

答案： 有用功；额外功；总功；$W_{总}=W_{有}+W_{额}$

2. 物理学中,将有用功和总功的比值叫作机械效率,写成公式就是$\eta = \frac{W_{有用}}{W_{总}} × 100\%$。

答案： 有用功和总功的比值，$\eta = \frac{W_{有用}}{W_{总}} × 100\%$

3. 使用机械时,由于额外功存在,所以总功______(大于/等于/小于)大于有用功。因此,机械效率总是______(大于/等于/小于)小于100%。

答案： 额外功；大于；小于

例题 如图11-5-1所示,用滑轮组将重2540N的货物提升1.7m。若不考虑摩擦,也不考虑滑轮和绳子所受的重力,则：

(1)绳端的拉力F是多少？
(2)绳端移动的距离是多少？
(3)若考虑摩擦、滑轮和绳子所受的重力,需在绳端施力800N,滑轮组的机械效率是多少？
解析 使用滑轮组时,重物G由n段绳子承担,提起重物G所用的力F就是重物G的n分之一；由于重物G是由n段绳子承担,当重物升高h时,绳末端移动的距离s= nh；若考虑摩擦、滑轮和绳子的物重,滑轮组的机械效率等于有用功和总功的比值。
(1)绳端的拉力
$ F = \frac{G}{n} = \frac{2540N}{4} = 635N $
(2)绳端移动的距离
$ s = nh = 4 × 1.7m = 6.8m $
(3)滑轮组的机械效率
$ \eta = \frac{W_{有用}}{W_{总}} × 100\% = \frac{Gh}{F's} = \frac{Gh}{F'nh} = \frac{G}{nF'} = \frac{2540}{4 × 800} × 100\% \approx 79\% $
说明 如何判断有用功、额外功、总功,是解机械效率有关问题的关键,解题时可以用机械做功的目的来分析。凡是用机械来升高物体的,使物体升高所做的功为有用功,且有$W_{有用} = Gh$,即有用功等于被升高的物体的重力与其被提升高度的乘积。凡是动力做的功就是总功,且有$W_{总} = Fs$,它等于力与机械在动力作用下移动的距离的乘积。用来克服摩擦和机械自身重力所做的功为额外功。$W_{额外} = W_{总} - W_{有用}$。

答案： 答题卡：
(1)
由图可知，承担物重的绳子段数$n = 4$，
根据公式$F=\frac{G}{n}$，可得绳端的拉力：
$F = \frac{2540N}{4}=635N$。
(2)
绳端移动的距离：
$s = nh=4×1.7m = 6.8m$。
(3)
根据公式$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{Gh}{F's}=\frac{Gh}{F'nh}=\frac{G}{nF'}$，可得滑轮组的机械效率：
$\eta=\frac{2540N}{4×800N}×100\%\approx79\%$。
结论：
(1)绳端的拉力$F$是$635N$；
(2)绳端移动的距离是$6.8m$；
(3)滑轮组的机械效率约是$79\%$。