《2025年课课练九年级物理上册苏科版》

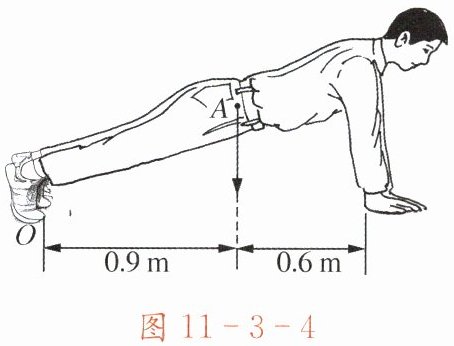
12. 如图11-3-4所示,某同学在做俯卧撑运动,若将他视为一个杠杆,他的重心在$A$点,重力为500N,则他将身体撑起,双手对地面的压力至少为300N；若他每次肩部上升的距离均为0.4m,则他一次俯卧撑做的功约120J。

答案： 300 120

13. 如图11-3-5所示,质量为1.2kg的无人机下方悬挂着一个质量为0.1kg的摄像机,它在10s内从地面匀速竖直上升了15m。无人机重为12N,上升的速度为1.5m/s,10s内无人机对摄像机所做的功为15J。($g$取10N/kg)

答案： 12 1.5 15

14. 假设步枪枪膛里火药爆炸产生的气体往外推子弹的力是11760N,把子弹从枪膛里推出共做了7291.2J的功。求枪膛的长。

答案： 0.62 m

15. 某人乘坐出租车在平直的公路上匀速行驶,出租车的牵引力为$3×10^3N$,图11-3-6为他乘车到达目的地时的车费发票。求：
(1)出租车行驶的时间。
(2)出租车行驶的速度。
(3)出租车在这段时间内所做的功。

答案： （1）300 s （2）20 m/s （3）1.8×10⁷ J

差动滑轮的原理
工厂里有一种特殊结构的滑轮,叫作差动滑轮(俗称“神仙葫芦”),它由两个直径相差不多的定滑轮和一个动滑轮组成,其示意图如图11-3-7所示。有了它,只需一个人就可以缓慢提升或移动很重的物体。
(1)设大定滑轮半径为$R$,小定滑轮半径为$r$($R稍大于r$),用力$F$拉绳,使两个定滑轮同轴转动一周,则图中绳子$A$点拉出的长度为2πR,绳子$B$点下降的长度为2πr,重物上升的高度为π(R-r)。
(2)设物重为$G$,则在两个定滑轮转动一周的过程中,拉力$F$做的功为2πRF,动滑轮对重物做的功为πG(R-r)。

答案： 1. ：
对于大定滑轮，根据圆的周长公式$C = 2\pi R$，当大定滑轮转动一周时，绳子$A$点拉出的长度$l_{A}=2\pi R$；
对于小定滑轮，根据圆的周长公式$C = 2\pi r$，当小定滑轮转动一周时，绳子$B$点下降的长度$l_{B}=2\pi r$；
动滑轮上升的高度$h$，由于动滑轮两侧绳子的变化，$h=\frac{l_{A}-l_{B}}{2}$（因为动滑轮省力费距离，绳子移动距离差的一半是物体上升高度），把$l_{A}=2\pi R$，$l_{B}=2\pi r$代入可得$h = \pi(R - r)$。
2. ：
根据功的计算公式$W = Fs$，拉力$F$做的功$W_{F}=F× l_{A}=2\pi RF$；
动滑轮对重物做的功$W_{G}=Gh$，把$h=\pi(R - r)$代入可得$W_{G}=G\pi(R - r)$。
故答案依次为：$2\pi R$；$2\pi r$；$\pi(R - r)$；$2\pi RF$；$G\pi(R - r)$。