《2025年单元评价卷宁波出版社六年级数学上册人教版》

1. 根据提供的圆作答。
(1)画出直径AB。
(2)圆周上任取一点C。
(3)连接AC,BC,量出∠ACB的度数。
(4)点C是圆上任意一点,你想到了什么呢？

答案：

(4) 点C是圆上任意一点：
根据测量结果，可以得出：半圆（或直径）所对的圆周角是直角，即在同一个圆中，直径所对的圆周角为90°。

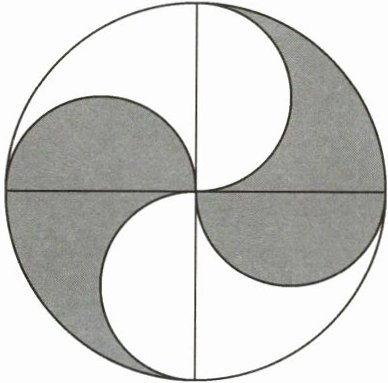
2. 如图是利用圆规和三角尺画出的图形。已知圆的半径是2厘米,求阴影部分的面积。

答案： 由图可知，大圆半径$ R = 2 $厘米，阴影部分由4个半径为$ r=\frac{R}{2}=1 $厘米的半圆组成。
每个半圆面积为$ \frac{1}{2}\pi r^{2} $，则4个半圆面积为：
$ 4×\frac{1}{2}\pi r^{2}=2\pi r^{2} $
将$ r = 1 $代入得：$ 2\pi×1^{2}=2\pi $（平方厘米）
$ 2\pi\approx2×3.14 = 6.28 $（平方厘米）
答案：$ 6.28 $平方厘米

3. 已知一个圆的半径是r,画一个圆内最大的正方形。
小明说：“如图,正方形里的每个三角形都是等腰直角三角形。”请你开动脑筋,帮助小明说明理由,你能想出几条理由呢？

答案： 1. 圆内最大的正方形的对角线等于圆的直径$2r$，设正方形与圆相交的四个顶点为$A$、$B$、$C$、$D$，圆心为$O$，连接$OA$、$OB$、$OC$、$OD$，$OA = OB=OC = OD=r$（圆的半径）。
在$\triangle OAB$中，$OA = OB$，$\angle OAB=\angle OBA = 45^{\circ}$（因为正方形对称，$\angle AOB = 90^{\circ}$，等腰三角形两底角相等，$(180^{\circ}-90^{\circ})÷2 = 45^{\circ}$），同理可证$\triangle OBC$、$\triangle OCD$、$\triangle ODA$中相关角的关系，且$OA = OB$，$OB = OC$，$OC = OD$，$OD = OA$，所以正方形里的每个三角形都是等腰直角三角形。
2. 因为圆的半径都相等，即$OA = OB = OC = OD$，在$\triangle OAB$中，$OA$和$OB$是圆的半径，长度为$r$，所以$OA = OB$，又因为正方形内接于圆，$\angle AOB = 90^{\circ}$，根据等腰直角三角形的定义（有一个角是直角且两条直角边相等的三角形是等腰直角三角形），$\triangle OAB$是等腰直角三角形，同理可证其他三个三角形也是等腰直角三角形。