《2025年课本配套练习五年级数学上册苏教版》

3. 有两根蜡烛，一根比较细，长 30 厘米，可以点 3 小时；一根比较粗，长 20 厘米，可以点 4 小时。同时点燃这两根蜡烛，几小时后，这两根蜡烛一样长？

()小时后，这两根蜡烛一样长。

答案： 细蜡烛每小时燃烧长度：$30÷3 = 10$（厘米/小时）
粗蜡烛每小时燃烧长度：$20÷4 = 5$（厘米/小时）
设$x$小时后两根蜡烛一样长。
$30 - 10x = 20 - 5x$
$10x - 5x = 30 - 20$
$5x = 10$
$x = 2$
2

4. 足球比赛中，胜一场得 3 分，平一场得 1 分，负一场得 0 分。希望小学足球队比赛两场，可能得多少分？（列举出所有可能的情况）

答案： 情况1：两场全胜，得分：3+3=6分
情况2：一胜一平，得分：3+1=4分
情况3：一胜一负，得分：3+0=3分
情况4：两场平局，得分：1+1=2分
情况5：一平一负，得分：1+0=1分
情况6：两场全负，得分：0+0=0分
可能得分为：0分、1分、2分、3分、4分、6分。

5. 王芳用 18 个边长 1 厘米的正方形拼成一个长方形，一共有多少种不同的拼法？

答案： 1. 长方形面积=长×宽=18平方厘米，正方形边长1厘米，面积1平方厘米，18个正方形总面积18平方厘米。
2. 求18的正整数因数对：
1×18=18，长18厘米，宽1厘米；
2×9=18，长9厘米，宽2厘米；
3×6=18，长6厘米，宽3厘米。
3. 因数对(6,3)与(3,6)、(9,2)与(2,9)、(18,1)与(1,18)为同一长方形，故不同拼法共3种。
结论：3种。

6. 如图，小华从家去科技馆，如果只能向东或向北走，一共有多少种不同的路线？

答案：

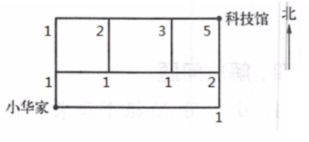
答：一共有5种不同的路线。

一列火车往返于南京和上海之间，中途停靠 6 个站，这列火车要准备多少种不同的车票？（假设车票只有起点或终点的不同，没有等次之分）

答案： 56 种