第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
9. 根据下面的图示,选择合适的条件和问题组成一道实际问题并解答。
①有苹果24个
②有橘子12个
③苹果的个数是梨的4倍
④橘子的个数是梨的4倍
⑤苹果的个数是梨的几倍
⑥橘子的个数是梨的几倍
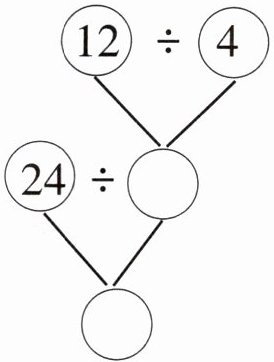
1. 首先组成实际问题:
有橘子12个,橘子的个数是梨的4倍,有苹果24个,苹果的个数是梨的几倍?
2. 然后解答:
解:先求梨的个数,因为橘子的个数是梨的4倍,橘子有12个,根据“已知一个数的几倍是多少,求这个数用除法”,可得梨的个数为12÷4 = 3(个)。
再求苹果个数是梨的几倍,苹果有24个,梨有3个,根据“求一个数是另一个数的几倍用除法”,可得24÷(12÷4)。
先算括号里的12÷4 = 3,再算24÷3 = 8。
所以苹果的个数是梨的8倍。
①有苹果24个
②有橘子12个
③苹果的个数是梨的4倍
④橘子的个数是梨的4倍
⑤苹果的个数是梨的几倍
⑥橘子的个数是梨的几倍

1. 首先组成实际问题:
有橘子12个,橘子的个数是梨的4倍,有苹果24个,苹果的个数是梨的几倍?
2. 然后解答:
解:先求梨的个数,因为橘子的个数是梨的4倍,橘子有12个,根据“已知一个数的几倍是多少,求这个数用除法”,可得梨的个数为12÷4 = 3(个)。
再求苹果个数是梨的几倍,苹果有24个,梨有3个,根据“求一个数是另一个数的几倍用除法”,可得24÷(12÷4)。
先算括号里的12÷4 = 3,再算24÷3 = 8。
所以苹果的个数是梨的8倍。
答案:
1. 首先组成实际问题:
有橘子$12$个,橘子的个数是梨的$4$倍,有苹果$24$个,苹果的个数是梨的几倍?
2. 然后解答:
解:先求梨的个数,因为橘子的个数是梨的$4$倍,橘子有$12$个,根据“已知一个数的几倍是多少,求这个数用除法”,可得梨的个数为$12÷4 = 3$(个)。
再求苹果个数是梨的几倍,苹果有$24$个,梨有$3$个,根据“求一个数是另一个数的几倍用除法”,可得$24÷(12÷4)$。
先算括号里的$12÷4 = 3$,再算$24÷3 = 8$。
所以苹果的个数是梨的$8$倍。
有橘子$12$个,橘子的个数是梨的$4$倍,有苹果$24$个,苹果的个数是梨的几倍?
2. 然后解答:
解:先求梨的个数,因为橘子的个数是梨的$4$倍,橘子有$12$个,根据“已知一个数的几倍是多少,求这个数用除法”,可得梨的个数为$12÷4 = 3$(个)。
再求苹果个数是梨的几倍,苹果有$24$个,梨有$3$个,根据“求一个数是另一个数的几倍用除法”,可得$24÷(12÷4)$。
先算括号里的$12÷4 = 3$,再算$24÷3 = 8$。
所以苹果的个数是梨的$8$倍。
10. 3位老师带领8名学生参观博物馆。如何购票最划算?
票价

票价

答案:
解析:本题考查的是利用四则运算解决实际问题,关键在于分别计算出不同购票方案所需的费用,然后进行比较,从而得出最划算的购票方式。
方案一:老师买成人票,学生买学生票。
老师有$3$位,成人票$15$元/人,根据“总价 = 单价×数量”,老师购票花费$15× 3 = 45$(元)。
学生有$8$名,学生票$7$元/人,同理可得学生购票花费$7× 8 = 56$(元)。
那么总共花费$45 + 56 = 101$(元)。
方案二:全部买团体票。
总人数为老师人数与学生人数之和,即$3 + 8 = 11$(人)。
团体票$10$元/人,所以全部买团体票花费$10× 11 = 110$(元)。
方案三:$3$位老师和$2$名学生组成$5$人买团体票,其余$8 - 2 = 6$(名)学生买学生票。
$5$人买团体票花费$10× 5 = 50$(元)。
$6$名学生买学生票花费$7× 6 = 42$(元)。
总共花费$50 + 42 = 92$(元)。
比较三种方案的费用:$92\lt 101\lt 110$。
答案:$3$位老师和$2$名学生买团体票,其余$6$名学生买学生票最划算。
方案一:老师买成人票,学生买学生票。
老师有$3$位,成人票$15$元/人,根据“总价 = 单价×数量”,老师购票花费$15× 3 = 45$(元)。
学生有$8$名,学生票$7$元/人,同理可得学生购票花费$7× 8 = 56$(元)。
那么总共花费$45 + 56 = 101$(元)。
方案二:全部买团体票。
总人数为老师人数与学生人数之和,即$3 + 8 = 11$(人)。
团体票$10$元/人,所以全部买团体票花费$10× 11 = 110$(元)。
方案三:$3$位老师和$2$名学生组成$5$人买团体票,其余$8 - 2 = 6$(名)学生买学生票。
$5$人买团体票花费$10× 5 = 50$(元)。
$6$名学生买学生票花费$7× 6 = 42$(元)。
总共花费$50 + 42 = 92$(元)。
比较三种方案的费用:$92\lt 101\lt 110$。
答案:$3$位老师和$2$名学生买团体票,其余$6$名学生买学生票最划算。
查看更多完整答案,请扫码查看


