《2025年新课程课堂同步练习册四年级数学上册苏教版》

一、先填上角的名称,并将各角按度数从大到小排列。

(周角)＞(平角)＞(钝角)＞(直角)＞(锐角)

答案： 解析：本题主要考查角的分类，包括周角、平角、钝角、直角和锐角，需要根据各类角的度数范围来确定图中角的名称，并按照度数从大到小的顺序进行排列。
答案如下：
角1是平角，角2是锐角，角3是周角，角4是钝角，角5是直角。
$(周角)＞(平角)＞(钝角)＞(直角)＞(锐角)$。

1. 90°的角是(直)角,锐角小于(90)°,平角等于(180)°,周角等于(360)°。

答案： 解析：本题考查角的分类以及各类角的度数范围。
答案：
直；$90$；$180$；$360$。

2. (1)角的大小与两边叉开的大小有关系。
(2)用一副三角板两角相拼,拼出的最小角是15°,最大角是180°。

答案： 解析：
(1) 这一题考查角的基本性质，即角的大小是由其两边叉开的大小决定的。
(2) 这一题考查对三角板角度的理解以及角度的加法。一副常规的三角板有两个，其中一个的角度为$30^\circ, 60^\circ, 90^\circ$，另一个的角度为$45^\circ, 45^\circ, 90^\circ$。为了得到最小和最大的角，需要考虑如何组合这些角度。
答案：
(1) 角的大小与(两边叉开的大小)有关系。
(2) 用一副三角板两角相拼, 拼出的最小角是
(15)°（由$45^\circ$和$30^\circ$的差得到），最大角是
(180)°（由$90^\circ$和$90^\circ$的和得到）。

3. 左图中,∠3= (90)°,如果∠1 = 60°,则∠2 = (30)°。

答案： 解析：根据图中的直角标识，可知∠3为直角，即$∠3 = 90^\circ$。
已知$∠1 = 60^\circ$，$∠1$、$∠2$、$∠3$组成平角，平角为$180^\circ$，
所以可以通过平角的度数减去$∠1$和$∠3$的度数来求得$∠2$的度数。
答案：$∠3 = 90^\circ$；
$∠2 = 180^\circ - 90^\circ - 60^\circ = 30^\circ$。

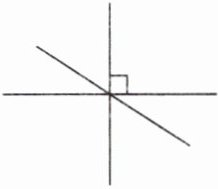
4. 数一数,右图中有(4)个直角,(2)个平角。

答案： 4；2

三、以下面的射线为角的一条边,用量角器分别画出65°、108°和135°的角。

答案： 1. 画$65^{\circ}$角：
步骤：
先将量角器的中心与射线的端点重合，$0^{\circ}$刻度线与已知射线重合。
在量角器$65^{\circ}$刻度线的地方点一个点。
以射线的端点为端点，通过刚才点的点，再画一条射线，这样就画出了$65^{\circ}$的角。
2. 画$108^{\circ}$角：
步骤：
把量角器的中心与射线的端点重合，$0^{\circ}$刻度线与已知射线重合。
在量角器$108^{\circ}$刻度线的位置点一个点。
最后以射线的端点为端点，经过点的点画射线，得到$108^{\circ}$的角。
3. 画$135^{\circ}$角：
步骤：
使量角器的中心和射线的端点重合，$0^{\circ}$刻度线与已知射线重合。
在量角器$135^{\circ}$刻度线处点一个点。
以射线的端点为端点，通过该点画射线，即画出$135^{\circ}$的角。
（由于是画图题，这里主要阐述画图步骤，实际操作时按照上述步骤用量角器完成画图即可）

四、辨析题。
小乐说：“周角是一条射线。”你同意他的观点吗？说一说你的理由。

答案： 解析：题目考查角的定义和周角的性质。需要理解角是由有公共端点的两条射线组成，周角是两条射线完全重合的特殊情况。
答案：不同意。周角不是一条射线，而是由有公共端点的两条射线完全重合形成的，只是这两条射线重合在一起，看起来像一条射线，但实际上它仍然是一个角，且角度为360度。

五、按要求分一分,画一画。

答案： 本题可根据锐角、直角、钝角的定义，结合角的大小关系进行画图。
1. 分成$1$个锐角和$1$个直角
直角是$90^{\circ}$的角，锐角是大于$0^{\circ}$而小于$90^{\circ}$的角。
用三角板的直角，在给定的钝角中，从钝角的顶点出发，画一条射线，使其中一个角为直角，另一个角则为锐角。
2. 分成$1$个锐角和$1$个钝角
钝角是大于$90^{\circ}$小于$180^{\circ}$的角，锐角是大于$0^{\circ}$而小于$90^{\circ}$的角。
从钝角的顶点出发，画一条射线，使其中一个角大于$90^{\circ}$（为钝角），另一个角小于$90^{\circ}$（为锐角）。
3. 分成$2$个锐角
锐角是大于$0^{\circ}$而小于$90^{\circ}$的角。
从钝角的顶点出发，画一条射线，使分成的两个角都小于$90^{\circ}$，即都为锐角。
由于无法直接为您画出图形，您可以根据上述描述，使用直尺和三角板等工具完成画图操作。
综上，按照锐角、直角、钝角的定义，**从钝角的顶点出发画射线**，即可完成相应的分割（具体图形以实际绘制为准）。