第23页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
5. 下面是3个容量不同的杯子。
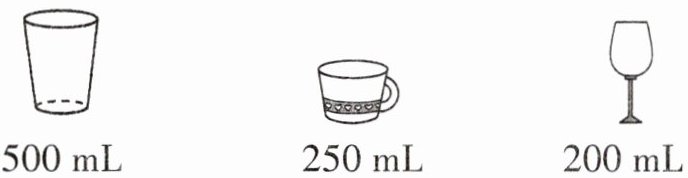
1升水可以倒满( 杯;倒满(
杯;倒满( 杯;倒满(
杯;倒满( 杯。
杯。

1升水可以倒满(
2
) 杯;倒满(
杯;倒满(4
) 杯;倒满(
杯;倒满(5
) 杯。
杯。
答案:
解析:本题考查单位换算以及除法运算。
因为$1$升$ = 1000$毫升。
对于$500$毫升的杯子:$1000÷500 = 2$(杯),即$1$升水可以倒满$2$个$500$毫升的杯子。
对于$250$毫升的杯子:$1000÷250 = 4$(杯),即$1$升水可以倒满$4$个$250$毫升的杯子。
对于$200$毫升的杯子:$1000÷200 = 5$(杯),即$1$升水可以倒满$5$个$200$毫升的杯子。
答案:2;4;5。
因为$1$升$ = 1000$毫升。
对于$500$毫升的杯子:$1000÷500 = 2$(杯),即$1$升水可以倒满$2$个$500$毫升的杯子。
对于$250$毫升的杯子:$1000÷250 = 4$(杯),即$1$升水可以倒满$4$个$250$毫升的杯子。
对于$200$毫升的杯子:$1000÷200 = 5$(杯),即$1$升水可以倒满$5$个$200$毫升的杯子。
答案:2;4;5。
6. 根据试商情况,写出各题应商几。


9
4
答案:
本题可根据整数除法的试商方法,结合余数与除数的关系来确定商。
第一题:$\frac{446}{47}$
试商时把$47$看作$50$,商$8$,计算$47×8 = 376$,然后用被除数$446$减去$376$得余数:$446 - 376=70$。
由于余数$70\gt47$,说明商$8$小了,所以应该商$9$。
第二题:$\frac{400}{84}$
试商时把$84$看作$80$,商$5$,计算$84×5 = 420$,$420\gt400$,说明商$5$大了,所以应该商$4$。
综上,答案依次为$\boldsymbol{9}$、$\boldsymbol{4}$。
第一题:$\frac{446}{47}$
试商时把$47$看作$50$,商$8$,计算$47×8 = 376$,然后用被除数$446$减去$376$得余数:$446 - 376=70$。
由于余数$70\gt47$,说明商$8$小了,所以应该商$9$。
第二题:$\frac{400}{84}$
试商时把$84$看作$80$,商$5$,计算$84×5 = 420$,$420\gt400$,说明商$5$大了,所以应该商$4$。
综上,答案依次为$\boldsymbol{9}$、$\boldsymbol{4}$。
7. □÷46=17……☆,☆最大是(
45
),这时□是(827
)。
答案:
解析:本题主要考查有余数的除法中余数和被除数的计算。在有余数的除法中,余数一定小于除数,所以余数☆最大为$46 - 1 = 45$。再根据被除数等于商乘除数加余数,可求出被除数□的值。
答案:$45$;$827$。
答案:$45$;$827$。
8. 每盒装有3小袋消毒湿巾,4盒共120元。算式120÷4表示(
一盒消毒湿巾的价钱
)。
答案:
解析:本题考查整数的除法运算。
题目给出了每盒装有3小袋消毒湿巾,4盒共120元。算式120÷4是通过将总价120元除以盒数4来计算每盒消毒湿巾的价格。
答案:一盒消毒湿巾的价钱。
题目给出了每盒装有3小袋消毒湿巾,4盒共120元。算式120÷4是通过将总价120元除以盒数4来计算每盒消毒湿巾的价格。
答案:一盒消毒湿巾的价钱。
9. 根据a÷b=12写出下面各题的商。
(a÷2)÷b=
(a÷2)÷b=
6
(a×4)÷b=48
(a÷6)÷(b÷6)=12
答案:
6
48
12
48
12
10. 如果2□5÷26的商的末尾有0,□里最小填(
6
),最大填(8
)。
答案:
6,8
1. 下面的算式中,(
A.314÷37
B.341÷73
C.413÷39
D.709÷72
C
)的商是两位数。A.314÷37
B.341÷73
C.413÷39
D.709÷72
答案:
C
2. 在检验310÷76=4……6时,不可采用(
A.76×4+6
B.(310-6)÷4
C.(310+6)÷4
D.(310-6)÷76
C
)进行验算。A.76×4+6
B.(310-6)÷4
C.(310+6)÷4
D.(310-6)÷76
答案:
在有余数的除法中,验算方法有:商×除数+余数=被除数,(被除数-余数)÷商=除数,(被除数-余数)÷除数=商。
选项A:76×4+6,符合商×除数+余数=被除数,可验算。
选项B:(310-6)÷4,符合(被除数-余数)÷商=除数,可验算。
选项C:(310+6)÷4,不符合有余数除法的验算方法,不可验算。
选项D:(310-6)÷76,符合(被除数-余数)÷除数=商,可验算。
答案:C
选项A:76×4+6,符合商×除数+余数=被除数,可验算。
选项B:(310-6)÷4,符合(被除数-余数)÷商=除数,可验算。
选项C:(310+6)÷4,不符合有余数除法的验算方法,不可验算。
选项D:(310-6)÷76,符合(被除数-余数)÷除数=商,可验算。
答案:C
3. 一个容器的容量是4升。将8杯同样多的豆浆全部倒入这个空的容器后,容器还未被装满。每杯豆浆可能是(
A.600
B.550
C.500
D.450
D
)毫升。A.600
B.550
C.500
D.450
答案:
4升=4000毫升
4000÷8=500(毫升)
因为容器未装满,所以每杯豆浆容量小于500毫升。
D
4000÷8=500(毫升)
因为容器未装满,所以每杯豆浆容量小于500毫升。
D
4. 根据126÷42=3,可以得出下面算式(
A.252÷84
B.378÷84
C.42÷21
D.63÷14
A
)的商也是3。A.252÷84
B.378÷84
C.42÷21
D.63÷14
答案:
解析:本题可根据商不变的规律来判断各个选项的商是否为$3$。商不变的规律为:被除数和除数同时乘或除以相同的数($0$除外),商不变。
选项A:在$126÷42$中,被除数$126$变为$252$,$252÷126 = 2$,即被除数乘$2$;除数$42$变为$84$,$84÷42 = 2$,即除数也乘$2$。被除数和除数同时乘$2$,根据商不变的规律,商不变,所以$252÷84 = 3$。
选项B:被除数$126$变为$378$,$378÷126 = 3$,即被除数乘$3$;除数$42$变为$84$,$84÷42 = 2$,即除数乘$2$。被除数和除数乘的数不同,商改变,$378÷84 = 4.5\neq3$。
选项C:被除数$126$变为$42$,$42÷126=\frac{1}{3}$,即被除数除以$3$;除数$42$变为$21$,$21÷42=\frac{1}{2}$,即除数除以$2$。被除数和除数除以的数不同,商改变,$42÷21 = 2\neq3$。
选项D:被除数$126$变为$63$,$63÷126=\frac{1}{2}$,即被除数除以$2$;除数$42$变为$14$,$14÷42=\frac{1}{3}$,即除数除以$3$。被除数和除数除以的数不同,商改变,$63÷14 = 4.5\neq3$。
答案:A
选项A:在$126÷42$中,被除数$126$变为$252$,$252÷126 = 2$,即被除数乘$2$;除数$42$变为$84$,$84÷42 = 2$,即除数也乘$2$。被除数和除数同时乘$2$,根据商不变的规律,商不变,所以$252÷84 = 3$。
选项B:被除数$126$变为$378$,$378÷126 = 3$,即被除数乘$3$;除数$42$变为$84$,$84÷42 = 2$,即除数乘$2$。被除数和除数乘的数不同,商改变,$378÷84 = 4.5\neq3$。
选项C:被除数$126$变为$42$,$42÷126=\frac{1}{3}$,即被除数除以$3$;除数$42$变为$21$,$21÷42=\frac{1}{2}$,即除数除以$2$。被除数和除数除以的数不同,商改变,$42÷21 = 2\neq3$。
选项D:被除数$126$变为$63$,$63÷126=\frac{1}{2}$,即被除数除以$2$;除数$42$变为$14$,$14÷42=\frac{1}{3}$,即除数除以$3$。被除数和除数除以的数不同,商改变,$63÷14 = 4.5\neq3$。
答案:A
查看更多完整答案,请扫码查看


