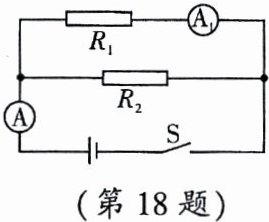
18.在如图所示的电路中,电阻$R_1$的阻值为10Ω。闭合开关S,电流表$A_1$的示数为0.3A,电流表A的示数为0.5A。求:
(1)电源电压;
(2)电阻$R_2$的阻值。
(1)电源电压;
(2)电阻$R_2$的阻值。

答案:
解:
(1)由图知,R₁与R₂并联,电流表A₁测R₁支路电流,电流表A测干路电流。
电源电压U=U₁=I₁R₁=0.3A×10Ω=3V。
(2)通过R₂的电流I₂=I - I₁=0.5A - 0.3A=0.2A,
电阻R₂的阻值R₂=U/I₂=3V/0.2A=15Ω。
答:
(1)电源电压为3V;
(2)电阻R₂的阻值为15Ω。
(1)由图知,R₁与R₂并联,电流表A₁测R₁支路电流,电流表A测干路电流。
电源电压U=U₁=I₁R₁=0.3A×10Ω=3V。
(2)通过R₂的电流I₂=I - I₁=0.5A - 0.3A=0.2A,
电阻R₂的阻值R₂=U/I₂=3V/0.2A=15Ω。
答:
(1)电源电压为3V;
(2)电阻R₂的阻值为15Ω。
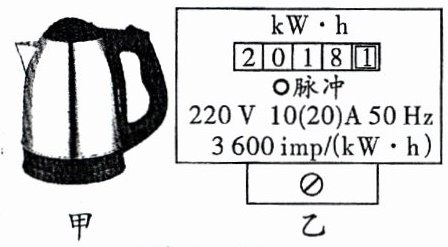
19.一家用电热水壶的额定功率为1210W,如甲图所示,为了粗测此热水壶的能效,在一次实际使用中,将家里其他用电器全部断开,用此水壶将2kg的水从20℃加热至100℃用了14min。期间,电能表上的脉冲指示灯闪烁了840次,表盘如乙图所示,其中3600imp/(kW·h)表示此电能表上接的用电器,每消耗1kW·h的电能,电能表的脉冲指示灯闪烁3600次,水的比热容$c= 4.2×10^{3}\ J/(kg·℃)$,计算在此次烧水的过程中:
(1)水吸收的热量;
(2)电热水壶的效率;
(3)电热水壶的实际工作电压。

(1)水吸收的热量;
(2)电热水壶的效率;
(3)电热水壶的实际工作电压。
答案:
【解析】:
本题主要考查了热量的计算、电能的计算、电功率的计算以及效率的计算等知识点。
(1)知道水的质量、水的比热容、水的初温和末温,利用吸热公式$Q_{吸} = cm(t - t_{0})$求出水吸收的热量。
(2)知道电能表上“$3600imp/(kW \cdot h)$”表示的含义,即每消耗$1kW \cdot h$的电能,电能表的脉冲指示灯闪烁$3600$次,据此求出脉冲指示灯闪烁了$840$次消耗的电能,又知道通电时间,利用$\eta = \frac{Q_{吸}}{W} × 100\%$求出电热水壶的效率。
(3)知道电热水壶的额定功率和额定电压,利用$P = \frac{U^{2}}{R}$求出电热水壶的电阻,再利用$P_{实} = \frac{W}{t}$求出电热水壶的实际功率,最后利用$P = \frac{U^{2}}{R}$的变形公式求出电热水壶的实际工作电压。
(1)水吸收的热量:$Q_{吸} = cm(t - t_{0}) = 4.2 × 10^{3} × 2 × (100 - 20) = 6.72 × 10^{5}J$。
(2)电能表上的脉冲指示灯闪烁了$840$次,则电热水壶消耗的电能为:$W = \frac{840}{3600} = \frac{7}{30}kW \cdot h = \frac{7}{30} × 3.6 × 10^{6} = 8.4 × 10^{5}J$,
电热水壶的效率:$\eta = \frac{Q_{吸}}{W} × 100\% = \frac{6.72 × 10^{5}}{8.4 × 10^{5}} × 100\% = 80\%$。
(3)由$P = \frac{U^{2}}{R}$可得,电热水壶的电阻:$R = \frac{U_{额}^{2}}{P_{额}} = \frac{(220)^{2}}{1210} = 40\Omega$,
电热水壶的实际功率:$P_{实} = \frac{W}{t} = \frac{8.4 × 10^{5}}{14 × 60} = 1000W$,
由$P = \frac{U^{2}}{R}$可得,电热水壶的实际工作电压:$U_{实} = \sqrt{P_{实}R} = \sqrt{1000 × 40} = 200V$。
【答案】:
(1)$6.72 × 10^{5}J$;(2)$80\%$;(3)$200V$。
本题主要考查了热量的计算、电能的计算、电功率的计算以及效率的计算等知识点。
(1)知道水的质量、水的比热容、水的初温和末温,利用吸热公式$Q_{吸} = cm(t - t_{0})$求出水吸收的热量。
(2)知道电能表上“$3600imp/(kW \cdot h)$”表示的含义,即每消耗$1kW \cdot h$的电能,电能表的脉冲指示灯闪烁$3600$次,据此求出脉冲指示灯闪烁了$840$次消耗的电能,又知道通电时间,利用$\eta = \frac{Q_{吸}}{W} × 100\%$求出电热水壶的效率。
(3)知道电热水壶的额定功率和额定电压,利用$P = \frac{U^{2}}{R}$求出电热水壶的电阻,再利用$P_{实} = \frac{W}{t}$求出电热水壶的实际功率,最后利用$P = \frac{U^{2}}{R}$的变形公式求出电热水壶的实际工作电压。
(1)水吸收的热量:$Q_{吸} = cm(t - t_{0}) = 4.2 × 10^{3} × 2 × (100 - 20) = 6.72 × 10^{5}J$。
(2)电能表上的脉冲指示灯闪烁了$840$次,则电热水壶消耗的电能为:$W = \frac{840}{3600} = \frac{7}{30}kW \cdot h = \frac{7}{30} × 3.6 × 10^{6} = 8.4 × 10^{5}J$,
电热水壶的效率:$\eta = \frac{Q_{吸}}{W} × 100\% = \frac{6.72 × 10^{5}}{8.4 × 10^{5}} × 100\% = 80\%$。
(3)由$P = \frac{U^{2}}{R}$可得,电热水壶的电阻:$R = \frac{U_{额}^{2}}{P_{额}} = \frac{(220)^{2}}{1210} = 40\Omega$,
电热水壶的实际功率:$P_{实} = \frac{W}{t} = \frac{8.4 × 10^{5}}{14 × 60} = 1000W$,
由$P = \frac{U^{2}}{R}$可得,电热水壶的实际工作电压:$U_{实} = \sqrt{P_{实}R} = \sqrt{1000 × 40} = 200V$。
【答案】:
(1)$6.72 × 10^{5}J$;(2)$80\%$;(3)$200V$。
查看更多完整答案,请扫码查看


