19.在研究“导体电流与电阻关系”的实验中,同学们利用阻值分别为5 Ω、10 Ω、15 Ω的定值电阻和变阻器进行探究,变阻器规格是“10 Ω 1 A”,电源电压为4.5 V并保持不变。按照电路图连接完成了如图甲所示的实物图。 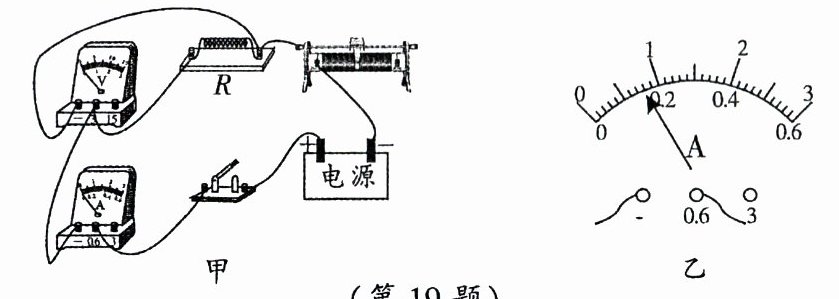
(1)正确连线后,闭合开关时发现,无论怎样移动滑片电流表示数均为0,电压表指针向右偏转且超过满刻度,原因可能是______
(2)先接入15 Ω的电阻,调节滑片使电压表示数为3 V,观察到电流表示数如图乙所示,则电流表示数为______
(3)分析三次的实验数据,可得出电流与电阻的关系是:______
(4)王强同学继续探究:他用了30 Ω的定值电阻代替原来的电阻实验,发现无论怎样移动滑片都不能满足电压表示数为3 V,原因是______

(1)正确连线后,闭合开关时发现,无论怎样移动滑片电流表示数均为0,电压表指针向右偏转且超过满刻度,原因可能是______
定值电阻R断路
。 (2)先接入15 Ω的电阻,调节滑片使电压表示数为3 V,观察到电流表示数如图乙所示,则电流表示数为______
0.2
A;用10 Ω电阻代替15 Ω电阻接入电路,应将滑片向______左
端(选填“左”或“右”)移动,才能使电压表示数保持3 V,并记录下电流表示数为0.3 A;用5 Ω电阻代替10 Ω电阻接入电路,正确操作,电流表示数为0.6 A。 (3)分析三次的实验数据,可得出电流与电阻的关系是:______
在电压一定时,电流与电阻成反比
。 (4)王强同学继续探究:他用了30 Ω的定值电阻代替原来的电阻实验,发现无论怎样移动滑片都不能满足电压表示数为3 V,原因是______
滑动变阻器的最大阻值太小
;要使电压表示数保持3 V不变,要求变阻器的最大阻值最少为______15
Ω。
答案:
【解析】:
(1)无论怎样移动滑片电流表示数均为0,说明电路存在断路性故障。电压表指针向右偏转且超过满刻度,说明电压表与电源两极是连通的,由此可判断出故障原因可能是定值电阻$R$断路。
(2)由图乙可知,电流表的量程为$0 - 0.6A$,分度值为$0.02A$,所以电流表示数为$0.2A$。
根据串联电路分压原理,当用$10\Omega$电阻代替$15\Omega$电阻接入电路时,电阻变小,其两端电压变小,要保持电阻两端电压不变,应减小滑动变阻器接入电路的电阻,即滑片向左移动。
(3)分析三次实验数据,电阻分别为$5\Omega$、$10\Omega$、$15\Omega$,对应的电流分别为$0.6A$、$0.3A$、$0.2A$,可以发现:在电压一定时,电流与电阻成反比。
(4)电源电压为$4.5V$,当接入$30\Omega$的定值电阻时,要使电压表示数为$3V$,则滑动变阻器两端电压为$4.5V - 3V = 1.5V$。
根据串联电路分压原理$\frac{U_{R}}{U_{滑}}=\frac{R}{R_{滑}}$,即$\frac{3V}{1.5V}=\frac{30\Omega}{R_{滑}}$,解得$R_{滑}=15\Omega$,而滑动变阻器的最大阻值为$10\Omega$,所以无论怎样移动滑片都不能满足电压表示数为$3V$。
要使电压表示数保持$3V$不变,要求变阻器的最大阻值最少为$15\Omega$。
【答案】:
(1)定值电阻$R$断路;
(2)$0.2$;左;
(3)在电压一定时,电流与电阻成反比;
(4)滑动变阻器的最大阻值太小;$15$。
(1)无论怎样移动滑片电流表示数均为0,说明电路存在断路性故障。电压表指针向右偏转且超过满刻度,说明电压表与电源两极是连通的,由此可判断出故障原因可能是定值电阻$R$断路。
(2)由图乙可知,电流表的量程为$0 - 0.6A$,分度值为$0.02A$,所以电流表示数为$0.2A$。
根据串联电路分压原理,当用$10\Omega$电阻代替$15\Omega$电阻接入电路时,电阻变小,其两端电压变小,要保持电阻两端电压不变,应减小滑动变阻器接入电路的电阻,即滑片向左移动。
(3)分析三次实验数据,电阻分别为$5\Omega$、$10\Omega$、$15\Omega$,对应的电流分别为$0.6A$、$0.3A$、$0.2A$,可以发现:在电压一定时,电流与电阻成反比。
(4)电源电压为$4.5V$,当接入$30\Omega$的定值电阻时,要使电压表示数为$3V$,则滑动变阻器两端电压为$4.5V - 3V = 1.5V$。
根据串联电路分压原理$\frac{U_{R}}{U_{滑}}=\frac{R}{R_{滑}}$,即$\frac{3V}{1.5V}=\frac{30\Omega}{R_{滑}}$,解得$R_{滑}=15\Omega$,而滑动变阻器的最大阻值为$10\Omega$,所以无论怎样移动滑片都不能满足电压表示数为$3V$。
要使电压表示数保持$3V$不变,要求变阻器的最大阻值最少为$15\Omega$。
【答案】:
(1)定值电阻$R$断路;
(2)$0.2$;左;
(3)在电压一定时,电流与电阻成反比;
(4)滑动变阻器的最大阻值太小;$15$。
20.现准备用“伏安法”测量标有“2.5 V”的小灯泡的电阻,实验室能提供的实验器材有:
A.待测小灯泡L(其正常工作时的电阻值约为10 Ω);
B.二节新的干电池串联(每节干电池的电压为1.5 V);
C.电压表一个(量程为0~3 V,0~15 V,电阻为5 kΩ);
D.电流表一个(量程为0~0.6 A,0~3 A,电阻为5 Ω);
E.滑动变阻器$R_0$(“50 Ω 1 A”);
F.开关S一个,导线若干。则:
(1)如果使用上述器材来测量小灯泡的电阻,那么,当小灯泡正常工作时,该电路中的电流约为
(2)由于电流表和电压表都有一定的电阻,严格来说将它们接入电路后,对电路都要产生一定的影响。那么,为了减少误差,在甲、乙所示的电路图(未画完)中,最好选
(3)根据以上选择的电路图,在丙图中用笔画线代替导线进行连线,使之成为能比较精确地测量出小灯泡电阻的电路(其中,部分导线已连接)。

(答案:图略)
(4)在实验中,某同学设计的实验报告及实验记录数据如下表所示。
|实验名称|用“伏安法”测量小灯泡的电阻|
|实验目的|练习使用电流表和电压表测量小灯泡的电阻|
|实验步骤|a.按照电路图连接电路,调节滑动变阻器的滑片P,使其连入电路中的
|实验记录| |
|电压U/V|电流I/A|电阻R/Ω|
|2.5|0.26|9.6|
|2.0|0.24|8.3|
|1.5|0.2|7.5|
|1.0|0.15|6.7|
①将实验步骤中的空格填写完整。
②从实验记录中可以看出,存在明显错误的记录数字是
③分析表中的数据发现灯丝的电阻是变化的,这是因为
A.待测小灯泡L(其正常工作时的电阻值约为10 Ω);
B.二节新的干电池串联(每节干电池的电压为1.5 V);
C.电压表一个(量程为0~3 V,0~15 V,电阻为5 kΩ);
D.电流表一个(量程为0~0.6 A,0~3 A,电阻为5 Ω);
E.滑动变阻器$R_0$(“50 Ω 1 A”);
F.开关S一个,导线若干。则:
(1)如果使用上述器材来测量小灯泡的电阻,那么,当小灯泡正常工作时,该电路中的电流约为
0.25
A。 (2)由于电流表和电压表都有一定的电阻,严格来说将它们接入电路后,对电路都要产生一定的影响。那么,为了减少误差,在甲、乙所示的电路图(未画完)中,最好选
甲
(选填“甲”或“乙”)。 (3)根据以上选择的电路图,在丙图中用笔画线代替导线进行连线,使之成为能比较精确地测量出小灯泡电阻的电路(其中,部分导线已连接)。

(答案:图略)
(4)在实验中,某同学设计的实验报告及实验记录数据如下表所示。
|实验名称|用“伏安法”测量小灯泡的电阻|
|实验目的|练习使用电流表和电压表测量小灯泡的电阻|
|实验步骤|a.按照电路图连接电路,调节滑动变阻器的滑片P,使其连入电路中的
阻值
最大。b.闭合开关,调节滑片P,使小灯泡两端的电压达到2.5
V,然后,测量电压开始逐次降低获得几组数据。c.根据测出的电压值和电流值,求出小灯泡的电阻。||实验记录| |
|电压U/V|电流I/A|电阻R/Ω|
|2.5|0.26|9.6|
|2.0|0.24|8.3|
|1.5|0.2|7.5|
|1.0|0.15|6.7|

①将实验步骤中的空格填写完整。
②从实验记录中可以看出,存在明显错误的记录数字是
0.15
。 ③分析表中的数据发现灯丝的电阻是变化的,这是因为
灯丝的电阻随温度的变化而变化
。
答案:
【解析】:
(1)已知灯泡正常工作时的电压$U_{L}=2.5V$,电阻$R_{L}\approx10\Omega$,
根据欧姆定律$I = \frac{U}{R}$,可得此时电路中的电流$I=\frac{U_{L}}{R_{L}}=\frac{2.5V}{10\Omega}=0.25A$。
电流表量程的选择:因为灯泡正常工作电流约为$0.25A$,所以电流表应选用$0 - 0.6A$量程。
(2)甲图是电流表外接法,乙图是电流表内接法。
灯泡电阻约为$10\Omega$,电压表电阻$R_{V}=5k\Omega = 5000\Omega$,电流表电阻$R_{A}=5\Omega$。
计算$\frac{R_{V}}{R_{L}}=\frac{5000\Omega}{10\Omega}=500$,$\frac{R_{L}}{R_{A}}=\frac{10\Omega}{5\Omega}=2$。
因为$\frac{R_{V}}{R_{L}}>\frac{R_{L}}{R_{A}}$,即电压表内阻远大于灯泡电阻,电流表分压作用较大,所以采用电流表外接法(甲图)误差较小。
(3)滑动变阻器已接了下面一个接线柱,应再接上面一个接线柱,如图所示(图略)。
(4)① 连接电路时,为了保护电路,滑动变阻器连入电路的阻值应最大。
闭合开关前,滑动变阻器滑片应移到阻值最大处,然后调节滑片$P$,使小灯泡两端的电压达到额定电压$2.5V$,再逐次降低电压获得几组数据。
② 由$R=\frac{U}{I}$计算电阻时,电流值$0.2A$对应的电压$U = 1.5V$,$R=\frac{1.5V}{0.2A}=7.5\Omega$;
电流值$0.24A$对应的电压$U = 2.0V$,$R=\frac{2.0V}{0.24A}\approx8.3\Omega$;
电流值$0.26A$对应的电压$U = 2.5V$,$R=\frac{2.5V}{0.26A}\approx9.6\Omega$;
而电流值$0.15A$对应的电压$U = 1.0V$,若按此计算$R=\frac{1.0V}{0.15A}\approx6.7\Omega$,
但根据前面数据规律,此组数据中电流值应为$0.16A$(因为电压从$1.5V$到$1.0V$,电阻变化有一定规律,$1.5V$时$0.2A$,$1.0V$时若电阻按前面规律变化,电流应为$0.16A$左右),
所以存在明显错误的记录数字是$0.15$。
③ 灯丝的电阻随温度的变化而变化,当灯泡两端电压变化时,通过灯泡的电流变化,根据$P = UI$,灯泡的实际功率变化,灯丝温度变化,所以灯丝电阻变化。
【答案】:
(1)$0.25$;
(2)甲;
(3)图略;
(4)① 阻值;$2.5$;
② $0.15$;
③ 灯丝的电阻随温度的变化而变化。
(1)已知灯泡正常工作时的电压$U_{L}=2.5V$,电阻$R_{L}\approx10\Omega$,
根据欧姆定律$I = \frac{U}{R}$,可得此时电路中的电流$I=\frac{U_{L}}{R_{L}}=\frac{2.5V}{10\Omega}=0.25A$。
电流表量程的选择:因为灯泡正常工作电流约为$0.25A$,所以电流表应选用$0 - 0.6A$量程。
(2)甲图是电流表外接法,乙图是电流表内接法。
灯泡电阻约为$10\Omega$,电压表电阻$R_{V}=5k\Omega = 5000\Omega$,电流表电阻$R_{A}=5\Omega$。
计算$\frac{R_{V}}{R_{L}}=\frac{5000\Omega}{10\Omega}=500$,$\frac{R_{L}}{R_{A}}=\frac{10\Omega}{5\Omega}=2$。
因为$\frac{R_{V}}{R_{L}}>\frac{R_{L}}{R_{A}}$,即电压表内阻远大于灯泡电阻,电流表分压作用较大,所以采用电流表外接法(甲图)误差较小。
(3)滑动变阻器已接了下面一个接线柱,应再接上面一个接线柱,如图所示(图略)。
(4)① 连接电路时,为了保护电路,滑动变阻器连入电路的阻值应最大。
闭合开关前,滑动变阻器滑片应移到阻值最大处,然后调节滑片$P$,使小灯泡两端的电压达到额定电压$2.5V$,再逐次降低电压获得几组数据。
② 由$R=\frac{U}{I}$计算电阻时,电流值$0.2A$对应的电压$U = 1.5V$,$R=\frac{1.5V}{0.2A}=7.5\Omega$;
电流值$0.24A$对应的电压$U = 2.0V$,$R=\frac{2.0V}{0.24A}\approx8.3\Omega$;
电流值$0.26A$对应的电压$U = 2.5V$,$R=\frac{2.5V}{0.26A}\approx9.6\Omega$;
而电流值$0.15A$对应的电压$U = 1.0V$,若按此计算$R=\frac{1.0V}{0.15A}\approx6.7\Omega$,
但根据前面数据规律,此组数据中电流值应为$0.16A$(因为电压从$1.5V$到$1.0V$,电阻变化有一定规律,$1.5V$时$0.2A$,$1.0V$时若电阻按前面规律变化,电流应为$0.16A$左右),
所以存在明显错误的记录数字是$0.15$。
③ 灯丝的电阻随温度的变化而变化,当灯泡两端电压变化时,通过灯泡的电流变化,根据$P = UI$,灯泡的实际功率变化,灯丝温度变化,所以灯丝电阻变化。
【答案】:
(1)$0.25$;
(2)甲;
(3)图略;
(4)① 阻值;$2.5$;
② $0.15$;
③ 灯丝的电阻随温度的变化而变化。
查看更多完整答案,请扫码查看


