2025年暑期升级训练浙江教育出版社八年级物理教科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑期升级训练浙江教育出版社八年级物理教科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
18. (10分)在“探究杠杆的平衡条件”实验中:
(1)小明安装好杠杆后,发现其左端下沉,如图甲所示,为使杠杆在水平位置平衡,应将平衡螺母向
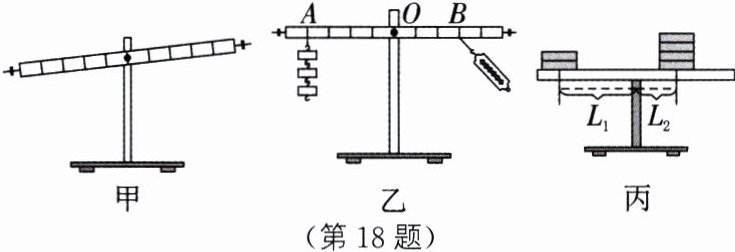
(2)如图乙所示,杠杆调节平衡后,在A处悬挂3个钩码,每个钩码重0.5 N。如果在B处施加一个拉力使杠杆在水平位置再次平衡,当方向为
(3)课后,小明制作了一个简易杠杆,调节杠杆在水平位置平衡,然后在它两边恰当位置分别放上不同数量的同种硬币,使其在水平位置再次平衡,如图丙所示,则力臂$L_1∶L_2 = $
(1)小明安装好杠杆后,发现其左端下沉,如图甲所示,为使杠杆在水平位置平衡,应将平衡螺母向
右
调节。
(2)如图乙所示,杠杆调节平衡后,在A处悬挂3个钩码,每个钩码重0.5 N。如果在B处施加一个拉力使杠杆在水平位置再次平衡,当方向为
竖直向下
时,拉力最小,大小为1
N。(3)课后,小明制作了一个简易杠杆,调节杠杆在水平位置平衡,然后在它两边恰当位置分别放上不同数量的同种硬币,使其在水平位置再次平衡,如图丙所示,则力臂$L_1∶L_2 = $
2∶3
;若两边同时各取走一枚硬币,则杠杆的左
端将下沉。
答案:
【解析】:
本题主要考查杠杆平衡条件的实验探究,包括杠杆的调平、最小力的判断与计算以及杠杆平衡条件的应用。
(1)在“探究杠杆的平衡条件”实验中,安装好杠杆后,若杠杆左端下沉,说明杠杆重心偏左,为使杠杆在水平位置平衡,应将平衡螺母向右调节,这样可以改变杠杆的重心位置,使杠杆达到平衡状态。
(2)根据杠杆平衡条件$F_1L_1 = F_2L_2$,在阻力和阻力臂一定时,动力臂越长,动力越小。在图乙中,当拉力方向垂直于杠杆向下时,动力臂最长,此时拉力最小。设每个钩码重$G = 0.5N$,一个格的长度为$L$,$A$处挂$3$个钩码,阻力$F_2 = 3×0.5N = 1.5N$,阻力臂$L_2 = 2L$,动力臂$L_1 = 3L$,根据杠杆平衡条件可得$F_1×3L = 1.5N×2L$,解得$F_1 = 1N$。
(3)设一个硬币的重力为$G$,在图丙中,根据杠杆平衡条件$F_1L_1 = F_2L_2$,左边$3$个硬币,右边$2$个硬币,即$3G× L_1 = 2G× L_2$,所以$L_1∶L_2 = 2∶3$。若两边同时各取走一枚硬币,左边$2G× L_1$,右边$G× L_2$,因为$L_1∶L_2 = 2∶3$,则$2G× L_1 = 2G×2 = 4G$,$G× L_2 = G×3 = 3G$,$4G>3G$,即左边力与力臂的乘积大于右边力与力臂的乘积,所以杠杆的左端将下沉。
【答案】:
(1)右;
(2)竖直向下;$1$;
(3)$2∶3$;左。
本题主要考查杠杆平衡条件的实验探究,包括杠杆的调平、最小力的判断与计算以及杠杆平衡条件的应用。
(1)在“探究杠杆的平衡条件”实验中,安装好杠杆后,若杠杆左端下沉,说明杠杆重心偏左,为使杠杆在水平位置平衡,应将平衡螺母向右调节,这样可以改变杠杆的重心位置,使杠杆达到平衡状态。
(2)根据杠杆平衡条件$F_1L_1 = F_2L_2$,在阻力和阻力臂一定时,动力臂越长,动力越小。在图乙中,当拉力方向垂直于杠杆向下时,动力臂最长,此时拉力最小。设每个钩码重$G = 0.5N$,一个格的长度为$L$,$A$处挂$3$个钩码,阻力$F_2 = 3×0.5N = 1.5N$,阻力臂$L_2 = 2L$,动力臂$L_1 = 3L$,根据杠杆平衡条件可得$F_1×3L = 1.5N×2L$,解得$F_1 = 1N$。
(3)设一个硬币的重力为$G$,在图丙中,根据杠杆平衡条件$F_1L_1 = F_2L_2$,左边$3$个硬币,右边$2$个硬币,即$3G× L_1 = 2G× L_2$,所以$L_1∶L_2 = 2∶3$。若两边同时各取走一枚硬币,左边$2G× L_1$,右边$G× L_2$,因为$L_1∶L_2 = 2∶3$,则$2G× L_1 = 2G×2 = 4G$,$G× L_2 = G×3 = 3G$,$4G>3G$,即左边力与力臂的乘积大于右边力与力臂的乘积,所以杠杆的左端将下沉。
【答案】:
(1)右;
(2)竖直向下;$1$;
(3)$2∶3$;左。
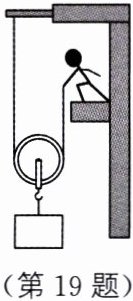
19. (8分)(扬州中考)如图所示,工人用动滑轮匀速提升重为400 N的窗玻璃,所用的竖直拉力为250 N,窗玻璃上升的高度为10 m,用时50 s。求:
(1)所做的有用功W有用。
(2)工人所用拉力的功率P。
(3)动滑轮的机械效率η。
(1)所做的有用功W有用。
(2)工人所用拉力的功率P。
(3)动滑轮的机械效率η。

答案:
【解析】:
本题主要考查了有用功、总功、功率和机械效率的计算,属于滑轮组相关的基础计算题。
(1)知道窗玻璃的重力和上升的高度,根据$W = Gh$求出有用功;
(2)根据$s = 2h$求出拉力移动的距离,根据$W = Fs$求出拉力做的总功,根据$P=\frac{W}{t}$求出拉力的功率;
(3)知道有用功和总功,根据$\eta=\frac{W_{有用}}{W_{总}}×100\%$求出动滑轮的机械效率。
【答案】:
解:(1)工人做的有用功:
$W_{有}=Gh = 400N×10m = 4000J$;
(2)使用动滑轮n = 2,绳子自由端移动的距离$s = 2h = 2×10m = 20m$,
工人做的总功:
$W_{总}=Fs = 250N×20m = 5000J$,
工人所用拉力的功率:
$P=\frac{W_{总}}{t}=\frac{5000J}{50s}=100W$;
(3)动滑轮的机械效率:
$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{4000J}{5000J}×100\% = 80\%$。
答:(1)所做的有用功为$4000J$;
(2)工人所用拉力的功率为$100W$;
(3)动滑轮的机械效率为$80\%$。
本题主要考查了有用功、总功、功率和机械效率的计算,属于滑轮组相关的基础计算题。
(1)知道窗玻璃的重力和上升的高度,根据$W = Gh$求出有用功;
(2)根据$s = 2h$求出拉力移动的距离,根据$W = Fs$求出拉力做的总功,根据$P=\frac{W}{t}$求出拉力的功率;
(3)知道有用功和总功,根据$\eta=\frac{W_{有用}}{W_{总}}×100\%$求出动滑轮的机械效率。
【答案】:
解:(1)工人做的有用功:
$W_{有}=Gh = 400N×10m = 4000J$;
(2)使用动滑轮n = 2,绳子自由端移动的距离$s = 2h = 2×10m = 20m$,
工人做的总功:
$W_{总}=Fs = 250N×20m = 5000J$,
工人所用拉力的功率:
$P=\frac{W_{总}}{t}=\frac{5000J}{50s}=100W$;
(3)动滑轮的机械效率:
$\eta=\frac{W_{有用}}{W_{总}}×100\%=\frac{4000J}{5000J}×100\% = 80\%$。
答:(1)所做的有用功为$4000J$;
(2)工人所用拉力的功率为$100W$;
(3)动滑轮的机械效率为$80\%$。
20. ★(8分)如图甲所示,在水平桌面上放置底面积为$100 cm^2、$质量为500 g的圆筒,筒内装有20 cm深的某液体。弹簧测力计下悬挂底面积为$60 cm^2、$高为10 cm的圆柱,从液面逐渐浸入直至浸没,弹簧测力计示数F随圆柱浸入液体的深度h的变化关系如图乙所示,g取10 N/kg,则:(可以忽略圆筒的厚度,该过程中液体没有从筒中溢出)

(1)圆柱浸没时受到的浮力是多少?
(2)筒内液体的密度是多少?
(3)当圆柱刚好浸没时,圆筒对桌面的压强是多少?

(1)圆柱浸没时受到的浮力是多少?
(2)筒内液体的密度是多少?
(3)当圆柱刚好浸没时,圆筒对桌面的压强是多少?
答案:
(1)由图乙可知,圆柱未浸入液体时弹簧测力计示数$F_1 = 17.4\ \text{N}$,即圆柱重力$G = 17.4\ \text{N}$;圆柱浸没时弹簧测力计示数$F_2 = 10\ \text{N}$。
根据称重法测浮力:$F_{\text{浮}}=G - F_2$,则$F_{\text{浮}}=17.4\ \text{N}-10\ \text{N}=7.4\ \text{N}$。
(2)圆柱浸没时,排开液体的体积等于圆柱的体积:$V_{\text{排}}=S_{\text{柱}}h_{\text{柱}}=60\ \text{cm}^2×10\ \text{cm}=600\ \text{cm}^3=6×10^{-4}\ \text{m}^3$。
由阿基米德原理$F_{\text{浮}}=\rho_{\text{液}}gV_{\text{排}}$得,$\rho_{\text{液}}=\frac{F_{\text{浮}}}{gV_{\text{排}}}$,代入数据:$\rho_{\text{液}}=\frac{7.4\ \text{N}}{10\ \text{N/kg}×6×10^{-4}\ \text{m}^3}\approx1.23×10^{3}\ \text{kg/m}^3$。
(3)圆筒质量$m_{\text{筒}}=500\ \text{g}=0.5\ \text{kg}$,圆筒重力$G_{\text{筒}}=m_{\text{筒}}g=0.5\ \text{kg}×10\ \text{N/kg}=5\ \text{N}$。
液体体积$V_{\text{液}}=S_{\text{筒}}h_{\text{液}}=100\ \text{cm}^2×20\ \text{cm}=2000\ \text{cm}^3=2×10^{-3}\ \text{m}^3$,液体重力$G_{\text{液}}=\rho_{\text{液}}gV_{\text{液}}=1.23×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}×2×10^{-3}\ \text{m}^3=24.6\ \text{N}$。
圆柱浸没时,圆筒对桌面的压力$F = G_{\text{筒}}+G_{\text{液}}+G - F_2$($G - F_2$为浮力,即液体对圆柱的作用力,根据力的作用是相互的,圆柱对液体的压力等于浮力),则$F=5\ \text{N}+24.6\ \text{N}+7.4\ \text{N}=37\ \text{N}$。
受力面积$S = 100\ \text{cm}^2=0.01\ \text{m}^2$,压强$p=\frac{F}{S}=\frac{37\ \text{N}}{0.01\ \text{m}^2}=3700\ \text{Pa}$。
(1)圆柱浸没时受到的浮力是$7.4\ \text{N}$;
(2)筒内液体的密度是$1.23×10^{3}\ \text{kg/m}^3$;
(3)当圆柱刚好浸没时,圆筒对桌面的压强是$3700\ \text{Pa}$。
(1)由图乙可知,圆柱未浸入液体时弹簧测力计示数$F_1 = 17.4\ \text{N}$,即圆柱重力$G = 17.4\ \text{N}$;圆柱浸没时弹簧测力计示数$F_2 = 10\ \text{N}$。
根据称重法测浮力:$F_{\text{浮}}=G - F_2$,则$F_{\text{浮}}=17.4\ \text{N}-10\ \text{N}=7.4\ \text{N}$。
(2)圆柱浸没时,排开液体的体积等于圆柱的体积:$V_{\text{排}}=S_{\text{柱}}h_{\text{柱}}=60\ \text{cm}^2×10\ \text{cm}=600\ \text{cm}^3=6×10^{-4}\ \text{m}^3$。
由阿基米德原理$F_{\text{浮}}=\rho_{\text{液}}gV_{\text{排}}$得,$\rho_{\text{液}}=\frac{F_{\text{浮}}}{gV_{\text{排}}}$,代入数据:$\rho_{\text{液}}=\frac{7.4\ \text{N}}{10\ \text{N/kg}×6×10^{-4}\ \text{m}^3}\approx1.23×10^{3}\ \text{kg/m}^3$。
(3)圆筒质量$m_{\text{筒}}=500\ \text{g}=0.5\ \text{kg}$,圆筒重力$G_{\text{筒}}=m_{\text{筒}}g=0.5\ \text{kg}×10\ \text{N/kg}=5\ \text{N}$。
液体体积$V_{\text{液}}=S_{\text{筒}}h_{\text{液}}=100\ \text{cm}^2×20\ \text{cm}=2000\ \text{cm}^3=2×10^{-3}\ \text{m}^3$,液体重力$G_{\text{液}}=\rho_{\text{液}}gV_{\text{液}}=1.23×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}×2×10^{-3}\ \text{m}^3=24.6\ \text{N}$。
圆柱浸没时,圆筒对桌面的压力$F = G_{\text{筒}}+G_{\text{液}}+G - F_2$($G - F_2$为浮力,即液体对圆柱的作用力,根据力的作用是相互的,圆柱对液体的压力等于浮力),则$F=5\ \text{N}+24.6\ \text{N}+7.4\ \text{N}=37\ \text{N}$。
受力面积$S = 100\ \text{cm}^2=0.01\ \text{m}^2$,压强$p=\frac{F}{S}=\frac{37\ \text{N}}{0.01\ \text{m}^2}=3700\ \text{Pa}$。
(1)圆柱浸没时受到的浮力是$7.4\ \text{N}$;
(2)筒内液体的密度是$1.23×10^{3}\ \text{kg/m}^3$;
(3)当圆柱刚好浸没时,圆筒对桌面的压强是$3700\ \text{Pa}$。
查看更多完整答案,请扫码查看


