《2025年暑假作业八年级广东人民出版社》

1. 已知等边三角形的边长为 2,则该三角形的面积为 (B)
A.$4\sqrt {3}$
B.$\sqrt {3}$
C.$2\sqrt {3}$
D.3

答案： B

2. 在平行四边形中,下列命题不成立的是 (A)
A.对角线长相等
B.相邻内角互补
C.两组对角分别相等
D.两组对边分别平行

答案： A

3. 能判定一个四边形是平行四边形的条件是 (C)
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角互补
C.一组对角相等,一组邻角互补
D.一组对角相等,另一组对角互补

答案： C

4. 下列条件中,能判定四边形 ABCD 是平行四边形的是 (B)
A.$AB= BC-CD$
B.$∠B+∠C= 180^{\circ },∠C+∠D= 180^{\circ }$
C.$AB= BC,CD= DA$
D.$∠A+∠B= 180^{\circ },∠C+∠D= 180^{\circ }$

答案： B

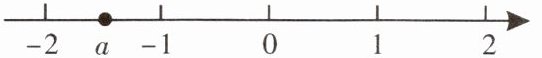
5. 实数 a 在数轴上的位置如图,化简$\sqrt {(a-1)^{2}}+a=$1.

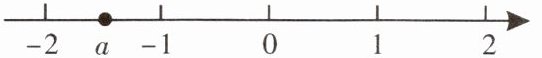
答案： 1

6. 一定质量的二氧化碳,当它的体积$V= 5m^{3}$时,它的密度$ρ=1.98kg/m^{3}$,则当$V= 10m^{3}$时,二氧化碳的密度为$0.99 kg/m^{3}$.

答案： $0.99 kg/m^{3}$

7. 在$□ ABCD$中,$∠A$的平分线将 CD 分为长为 4 cm 和 5 cm 的两条线段,则$□ ABCD$的周长为26 或 28cm.

答案： 26 或 28

8. 如图所示,$AB// CD,∠ACB= 90^{\circ }$,E 是 AB 的中点,$CE= CD$,DE 和 AC 相交于点 F. 求证:$DE⊥AC,AF= FC.$
证明：
∵∠ACB=90°，E是AB的中点，
∴CE=AE=EB（直角三角形斜边中线等于斜边一半）。
∵AB//CD，CE=CD，
∴CD=AE，且CD//AE。
∴四边形AECD是平行四边形（一组对边平行且相等的四边形是平行四边形）。
又∵CE=CD，
∴平行四边形AECD是菱形（邻边相等的平行四边形是菱形）。
∵菱形的对角线互相垂直且平分，
∴DE⊥AC，AF=FC。

答案： 证明：
∵∠ACB=90°，E是AB的中点，
∴CE=AE=EB（直角三角形斜边中线等于斜边一半）。
∵AB//CD，CE=CD，
∴CD=AE，且CD//AE。
∴四边形AECD是平行四边形（一组对边平行且相等的四边形是平行四边形）。
又
∵CE=CD，
∴平行四边形AECD是菱形（邻边相等的平行四边形是菱形）。
∵菱形的对角线互相垂直且平分，
∴DE⊥AC，AF=FC。

9. 如图所示,在$△ABC$中,$∠BAC= 90^{\circ }$,BD 平分$∠ABC,AG⊥BC$,且 BD,AG 相交于点 E,$DF⊥BC$,连接 EF. 求证:四边形 AEFD 是菱形.

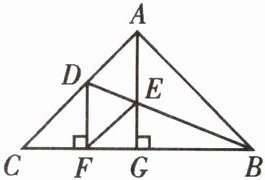
证明：
∵BD平分∠ABC，∠BAC=90°，DF⊥BC，
∴AD=DF（角平分线性质），∠BAD=∠BFD=90°。
在△ABD和△FBD中，
$\left\{\begin{array}{l} ∠BAD=∠BFD \\ ∠ABD=∠FBD \\ BD=BD \end{array}\right.$，
∴△ABD≌△FBD（AAS）。
∵AG⊥BC，DF⊥BC，
∴AG//DF，∠DAG=∠DFG=90°。
∵∠AED=∠BEF，∠ABE+∠AEB=90°，∠FBE+∠BEG=90°，且∠ABE=∠FBE，
∴∠AEB=∠BEG=∠AED，
∴△AED中，∠DAE=∠ADE，
∴AE=AD。
又∵AD=DF，
∴AE=DF。
∵AG//DF且AE=DF，
∴四边形AEFD是平行四边形。
∵AD=DF，
∴平行四边形AEFD是菱形。

答案： 证明：
∵BD平分∠ABC，∠BAC=90°，DF⊥BC，
∴AD=DF（角平分线性质），∠BAD=∠BFD=90°。
在△ABD和△FBD中，
$\left\{\begin{array}{l} ∠BAD=∠BFD \\ ∠ABD=∠FBD \\ BD=BD \end{array}\right.$，
∴△ABD≌△FBD（AAS）。
∵AG⊥BC，DF⊥BC，
∴AG//DF，∠DAG=∠DFG=90°。
∵∠AED=∠BEF，∠ABE+∠AEB=90°，∠FBE+∠BEG=90°，且∠ABE=∠FBE，
∴∠AEB=∠BEG=∠AED，
∴△AED中，∠DAE=∠ADE，
∴AE=AD。
又
∵AD=DF，
∴AE=DF。
∵AG//DF且AE=DF，
∴四边形AEFD是平行四边形。
∵AD=DF，
∴平行四边形AEFD是菱形。