2025年暑假作业八年级广东人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业八年级广东人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 下列各组二次根式化简后,被开方数不同的是(
A.$-\sqrt{2}与\sqrt{\frac{1}{2}}$
B.$\sqrt{18}与\sqrt{72}$
C.$\sqrt{54}与\sqrt{1.5}$
D.$\sqrt{45}与2\sqrt{3}$
D
)A.$-\sqrt{2}与\sqrt{\frac{1}{2}}$
B.$\sqrt{18}与\sqrt{72}$
C.$\sqrt{54}与\sqrt{1.5}$
D.$\sqrt{45}与2\sqrt{3}$
答案:
D
2. 若$\sqrt{x - 1}+(y + 2)^{2}= 0$,则$(x + y)^{2025}$等于(
A.-1
B.1
C.32014
D.-32014
A
)A.-1
B.1
C.32014
D.-32014
答案:
A
3. 关于函数$y= \frac{1}{3}x$,下列结论中正确的是(
A.函数图象经过点$(1,3)$
B.函数图象经过第二、四象限
C.y 随 x 的增大而增大
D.不论 x 为何值,总有$y>0$
C
)A.函数图象经过点$(1,3)$
B.函数图象经过第二、四象限
C.y 随 x 的增大而增大
D.不论 x 为何值,总有$y>0$
答案:
C
4. 四边形中,有一组对角都是直角,则另一组对角(
A.都是锐角
B.都是钝角
C.一个锐角一个钝角
D.一个锐角一个钝角或两个直角
D
)A.都是锐角
B.都是钝角
C.一个锐角一个钝角
D.一个锐角一个钝角或两个直角
答案:
D
5. 若三角形中相等的两边长为 10,第三边长为 16,则第三边上的高为(
A.12
B.10
C.8
D.6
D
)A.12
B.10
C.8
D.6
答案:
D
6. 在四边形 ABCD 中,已知$∠A = 90^{\circ}$,$∠B$,$∠C$,$∠D的度数比为1:2:3$,则$∠B= $
$45^{\circ}$
,$∠C= $$90^{\circ}$
,$∠D= $$135^{\circ}$
.
答案:
$45^{\circ}$ $90^{\circ}$ $135^{\circ}$
7. 计算:$(-\sqrt{2})^{2}=$
2
;$\sqrt{(-\frac{2}{3})^{2}}=$$\frac{2}{3}$
;$-\sqrt{(-\frac{2}{5})^{2}}=$$-\frac{2}{5}$
.
答案:
2 $\frac{2}{3}$ $-\frac{2}{5}$
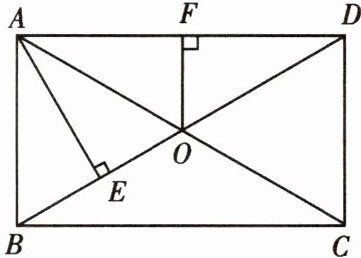
8. 如图所示,矩形 ABCD 的两对角线交于点 O,$AE⊥BD$,$OF⊥AD$,$BE:ED = 1:3$,$OF = 2cm$,求 AC 的长.
解:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠BAD=90°。
∵OF⊥AD,∠BAD=90°,
∴OF//AB,
∵O是BD中点,
∴F是AD中点,
∴OF是△ABD的中位线,
∴AB=2OF=2×2=
设BE=x,ED=3x,则BD=BE+ED=4x,
∴OB=OD=
∴OE=OB-BE=2x-x=x,即BE=OE=x。
∵AE⊥BD,
∴AE垂直平分OB,
∴AB=AO=
∴AC=2AO=2×4=
答:AC的长为

解:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠BAD=90°。
∵OF⊥AD,∠BAD=90°,
∴OF//AB,
∵O是BD中点,
∴F是AD中点,
∴OF是△ABD的中位线,
∴AB=2OF=2×2=
4
cm。 设BE=x,ED=3x,则BD=BE+ED=4x,
∴OB=OD=
2x
, ∴OE=OB-BE=2x-x=x,即BE=OE=x。
∵AE⊥BD,
∴AE垂直平分OB,
∴AB=AO=
4
cm, ∴AC=2AO=2×4=
8
cm。 答:AC的长为
8
cm。
答案:
解:
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠BAD=90°。
∵OF⊥AD,∠BAD=90°,
∴OF//AB,
∵O是BD中点,
∴F是AD中点,
∴OF是△ABD的中位线,
∴AB=2OF=2×2=4cm。
设BE=x,ED=3x,则BD=BE+ED=4x,
∴OB=OD=2x,
∴OE=OB-BE=2x-x=x,即BE=OE=x。
∵AE⊥BD,
∴AE垂直平分OB,
∴AB=AO=4cm,
∴AC=2AO=2×4=8cm。
答:AC的长为8cm。
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=OB=OD,∠BAD=90°。
∵OF⊥AD,∠BAD=90°,
∴OF//AB,
∵O是BD中点,
∴F是AD中点,
∴OF是△ABD的中位线,
∴AB=2OF=2×2=4cm。
设BE=x,ED=3x,则BD=BE+ED=4x,
∴OB=OD=2x,
∴OE=OB-BE=2x-x=x,即BE=OE=x。
∵AE⊥BD,
∴AE垂直平分OB,
∴AB=AO=4cm,
∴AC=2AO=2×4=8cm。
答:AC的长为8cm。
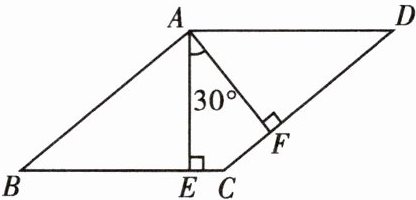
9. 如图所示,在$□ ABCD$中,AE,AF 分别为 BC,CD 上的高,垂足分别为 E,F,$∠EAF = 30^{\circ}$,求$□ ABCD$各内角的度数.
$□ABCD$各内角的度数分别为$∠B=∠D=$

$□ABCD$各内角的度数分别为$∠B=∠D=$
$30^{\circ}$
,$∠BAD=∠C=$$150^{\circ}$
。
答案:
解:在$□ABCD$中,$AE$、$AF$分别为$BC$、$CD$上的高,
$\therefore \angle AEC = \angle AFC = 90^{\circ}$。
在四边形$AECF$中,$\angle EAF = 30^{\circ}$,
$\angle C = 360^{\circ} - \angle AEC - \angle AFC - \angle EAF = 360^{\circ} - 90^{\circ} - 90^{\circ} - 30^{\circ} = 150^{\circ}$。
$\because$四边形$ABCD$是平行四边形,
$\therefore \angle BAD = \angle C = 150^{\circ}$,$AD// BC$,
$\therefore \angle B + \angle BAD = 180^{\circ}$,
$\angle B = 180^{\circ} - \angle BAD = 180^{\circ} - 150^{\circ} = 30^{\circ}$,
$\angle D = \angle B = 30^{\circ}$。
综上,$□ABCD$各内角的度数分别为$\angle B = \angle D = 30^{\circ}$,$\angle BAD = \angle C = 150^{\circ}$。
$\therefore \angle AEC = \angle AFC = 90^{\circ}$。
在四边形$AECF$中,$\angle EAF = 30^{\circ}$,
$\angle C = 360^{\circ} - \angle AEC - \angle AFC - \angle EAF = 360^{\circ} - 90^{\circ} - 90^{\circ} - 30^{\circ} = 150^{\circ}$。
$\because$四边形$ABCD$是平行四边形,
$\therefore \angle BAD = \angle C = 150^{\circ}$,$AD// BC$,
$\therefore \angle B + \angle BAD = 180^{\circ}$,
$\angle B = 180^{\circ} - \angle BAD = 180^{\circ} - 150^{\circ} = 30^{\circ}$,
$\angle D = \angle B = 30^{\circ}$。
综上,$□ABCD$各内角的度数分别为$\angle B = \angle D = 30^{\circ}$,$\angle BAD = \angle C = 150^{\circ}$。
查看更多完整答案,请扫码查看


