2025年暑假作业八年级广东人民出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业八年级广东人民出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 甲、乙两人各射靶 5 次,已知甲所中环数是 8,7,9,7,9,乙所中环数的平均数是 8,方差 $ s^{2}_{乙}= 0.4 $,那么,对甲、乙的射击成绩判断正确的是(
A.甲的射击成绩较稳定
B.乙的射击成绩较稳定
C.甲、乙的射击成绩同样稳定
D.甲、乙的射击成绩无法比较
B
)A.甲的射击成绩较稳定
B.乙的射击成绩较稳定
C.甲、乙的射击成绩同样稳定
D.甲、乙的射击成绩无法比较
答案:
B
2. 如图,$ P_{1} $,$ P_{2} $,$ P_{3} $ 是双曲线上的三点,过这三点分别作 $ y $ 轴的垂线,得到三个三角形 $ \triangle P_{1}A_{1}O $,$ \triangle P_{2}A_{2}O $,$ \triangle P_{3}A_{3}O $,设它们的面积分别是 $ S_{1} $,$ S_{2} $,$ S_{3} $,则(
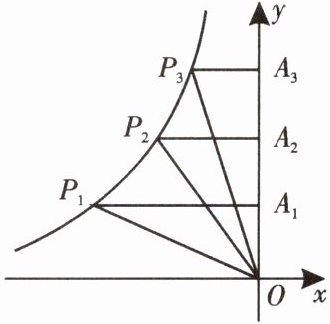
A.$ S_{1} \lt S_{2} \lt S_{3} $
B.$ S_{2} \lt S_{1} \lt S_{3} $
C.$ S_{1} \lt S_{3} \lt S_{2} $
D.$ S_{1}= S_{2}= S_{3} $
D
)
A.$ S_{1} \lt S_{2} \lt S_{3} $
B.$ S_{2} \lt S_{1} \lt S_{3} $
C.$ S_{1} \lt S_{3} \lt S_{2} $
D.$ S_{1}= S_{2}= S_{3} $
答案:
D
3. 在 $ \text{Rt}\triangle ABC $ 中,$ \angle C = 90^{\circ} $。(1)若 $ a = 10 $,$ b = 24 $,则 $ c = $
26
;(2)若 $ a = 12 $,$ b = 16 $,则 $ \triangle ABC $ 的周长为48
。
答案:
(1) 26
(2) 48
(1) 26
(2) 48
4. 一组数据是 1,2,3,3,6,那么这组数据的极差是
5
,方差是2.8
。
答案:
5 2.8
5. 有一面积为 60 的梯形,其上底长是下底长的 $ \dfrac{1}{3} $,若下底长为 $ x $,高为 $ y $,则 $ y $ 与 $ x $ 的函数关系式为
$ y = \frac { 90 } { x } $
。
答案:
$ y = \frac { 90 } { x } $
6. $ \left(4\sqrt{6}-4\sqrt{\dfrac{1}{2}}+3\sqrt{8}\right)÷ 2\sqrt{2} $
答案:
解:$\left(4\sqrt{6} - 4\sqrt{\dfrac{1}{2}} + 3\sqrt{8}\right)÷ 2\sqrt{2}$
$=4\sqrt{6}÷2\sqrt{2} - 4\sqrt{\dfrac{1}{2}}÷2\sqrt{2} + 3\sqrt{8}÷2\sqrt{2}$
$=2\sqrt{3} - 4×\dfrac{\sqrt{2}}{2}÷2\sqrt{2} + 3×2\sqrt{2}÷2\sqrt{2}$
$=2\sqrt{3} - (2\sqrt{2}÷2\sqrt{2}) + (6\sqrt{2}÷2\sqrt{2})$
$=2\sqrt{3} - 1 + 3$
$=2\sqrt{3} + 2$
$=4\sqrt{6}÷2\sqrt{2} - 4\sqrt{\dfrac{1}{2}}÷2\sqrt{2} + 3\sqrt{8}÷2\sqrt{2}$
$=2\sqrt{3} - 4×\dfrac{\sqrt{2}}{2}÷2\sqrt{2} + 3×2\sqrt{2}÷2\sqrt{2}$
$=2\sqrt{3} - (2\sqrt{2}÷2\sqrt{2}) + (6\sqrt{2}÷2\sqrt{2})$
$=2\sqrt{3} - 1 + 3$
$=2\sqrt{3} + 2$
7. $ \sqrt{24}× \sqrt{\dfrac{1}{3}}-4\sqrt{\dfrac{1}{8}}× (1-\sqrt{2})^{0} $
答案:
解:原式$=\sqrt{24×\frac{1}{3}} - 4\sqrt{\frac{1}{8}}×1$
$=\sqrt{8} - 4×\frac{\sqrt{2}}{4}$
$=2\sqrt{2} - \sqrt{2}$
$=\sqrt{2}$
$=\sqrt{8} - 4×\frac{\sqrt{2}}{4}$
$=2\sqrt{2} - \sqrt{2}$
$=\sqrt{2}$
8. 如图所示,已知在 $ \triangle ABC $ 中,$ CD \perp AB $ 于点 $ D $,$ AC = 20 $,$ BC = 15 $,$ DB = 9 $。
(1)求 $ DC $ 的长。(
(2)求 $ AB $ 的长。(
(3)求证:$ \triangle ABC $ 是直角三角形。
证明:$\because AC=20$,$BC=15$,$AB=25$
$AC^{2}+BC^{2}=20^{2}+15^{2}=400 + 225=625$
$AB^{2}=25^{2}=625$
$\therefore AC^{2}+BC^{2}=AB^{2}$
$\therefore\triangle ABC$是直角三角形
(1)求 $ DC $ 的长。(
12
)(2)求 $ AB $ 的长。(
25
)(3)求证:$ \triangle ABC $ 是直角三角形。
证明:$\because AC=20$,$BC=15$,$AB=25$
$AC^{2}+BC^{2}=20^{2}+15^{2}=400 + 225=625$
$AB^{2}=25^{2}=625$
$\therefore AC^{2}+BC^{2}=AB^{2}$
$\therefore\triangle ABC$是直角三角形
答案:
(1)解:在$Rt\triangle CDB$中,$CD\perp AB$,$BC=15$,$DB=9$
由勾股定理得$DC^{2}+DB^{2}=BC^{2}$
$DC^{2}=BC^{2}-DB^{2}=15^{2}-9^{2}=225 - 81=144$
$\therefore DC=12$
(2)解:在$Rt\triangle CDA$中,$CD=12$,$AC=20$
由勾股定理得$AD^{2}+CD^{2}=AC^{2}$
$AD^{2}=AC^{2}-CD^{2}=20^{2}-12^{2}=400 - 144=256$
$\therefore AD=16$
$\because AB=AD + DB$
$\therefore AB=16 + 9=25$
(3)证明:$\because AC=20$,$BC=15$,$AB=25$
$AC^{2}+BC^{2}=20^{2}+15^{2}=400 + 225=625$
$AB^{2}=25^{2}=625$
$\therefore AC^{2}+BC^{2}=AB^{2}$
$\therefore\triangle ABC$是直角三角形
(1)解:在$Rt\triangle CDB$中,$CD\perp AB$,$BC=15$,$DB=9$
由勾股定理得$DC^{2}+DB^{2}=BC^{2}$
$DC^{2}=BC^{2}-DB^{2}=15^{2}-9^{2}=225 - 81=144$
$\therefore DC=12$
(2)解:在$Rt\triangle CDA$中,$CD=12$,$AC=20$
由勾股定理得$AD^{2}+CD^{2}=AC^{2}$
$AD^{2}=AC^{2}-CD^{2}=20^{2}-12^{2}=400 - 144=256$
$\therefore AD=16$
$\because AB=AD + DB$
$\therefore AB=16 + 9=25$
(3)证明:$\because AC=20$,$BC=15$,$AB=25$
$AC^{2}+BC^{2}=20^{2}+15^{2}=400 + 225=625$
$AB^{2}=25^{2}=625$
$\therefore AC^{2}+BC^{2}=AB^{2}$
$\therefore\triangle ABC$是直角三角形
查看更多完整答案,请扫码查看


