2025年轻松暑假复习加预习中国海洋大学出版社八年级数学54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社八年级数学54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
同类二次根式的定义:几个二次根式化成最简二次根式以后,如果被开方数①
判断同类二次根式的方法:首先将不是最简形式的二次根式化为最简二次根式,再看②
加减法:合并③
乘法:$\sqrt { a } \cdot \sqrt { b } = $④
除法:$\frac { \sqrt { a } } { \sqrt { b } } = $⑤
混合运算:先乘方,再乘除,然后算加减,二次根式的混合运算可类比⑥
相同
,这几个二次根式叫做同类二次根式。判断同类二次根式的方法:首先将不是最简形式的二次根式化为最简二次根式,再看②
被开方数
是否相同;注意:几个二次根式是否是同类二次根式,只与被开方数及根指数有关加减法:合并③
同类二次根式
——化成最简二次根式后,将同类二次根式分别合并,有括号的先去括号乘法:$\sqrt { a } \cdot \sqrt { b } = $④
$\sqrt{ab}$
$( a \geq 0 , b \geq 0 )$除法:$\frac { \sqrt { a } } { \sqrt { b } } = $⑤
$\sqrt{\frac{a}{b}}$
$( a \geq 0 , b > 0 )$混合运算:先乘方,再乘除,然后算加减,二次根式的混合运算可类比⑥
整式
的运算法则进行计算,能用乘法公式的要用乘法公式简便计算
答案:
①相同 ②被开方数 ③同类二次根式 ④$\sqrt{ab}$ ⑤$\sqrt{\frac{a}{b}}$ ⑥整式
1. 计算:$\sqrt { 12 } - \sqrt { 3 }$等于(
A.$\sqrt { 3 }$
B.$2 \sqrt { 3 }$
C.3
D.$4 \sqrt { 3 }$
A
)A.$\sqrt { 3 }$
B.$2 \sqrt { 3 }$
C.3
D.$4 \sqrt { 3 }$
答案:
A
2. (2024·湖北模拟)下列计算正确的是(
A.$\sqrt { 5 } - \sqrt { 3 } = \sqrt { 2 }$
B.$\sqrt { ( - 2 ) ^ { 2 } } = - 2$
C.$a ^ { 5 } ÷ a ^ { 2 } = a ^ { 3 }$
D.$( a b ^ { 2 } ) ^ { 3 } = a b ^ { 6 }$
C
)A.$\sqrt { 5 } - \sqrt { 3 } = \sqrt { 2 }$
B.$\sqrt { ( - 2 ) ^ { 2 } } = - 2$
C.$a ^ { 5 } ÷ a ^ { 2 } = a ^ { 3 }$
D.$( a b ^ { 2 } ) ^ { 3 } = a b ^ { 6 }$
答案:
C
3. (2021·泰州)下列各组二次根式中,化简后是同类二次根式的是(
A.$\sqrt { 8 }与\sqrt { 3 }$
B.$\sqrt { 2 }与\sqrt { 12 }$
C.$\sqrt { 5 }与\sqrt { 15 }$
D.$\sqrt { 75 }与\sqrt { 27 }$
D
)A.$\sqrt { 8 }与\sqrt { 3 }$
B.$\sqrt { 2 }与\sqrt { 12 }$
C.$\sqrt { 5 }与\sqrt { 15 }$
D.$\sqrt { 75 }与\sqrt { 27 }$
答案:
D
4. (江苏中考)下列各数中与$2 + \sqrt { 3 }$的积是有理数的是(
A.$2 + \sqrt { 3 }$
B.2
C.$\sqrt { 3 }$
D.$2 - \sqrt { 3 }$
D
)A.$2 + \sqrt { 3 }$
B.2
C.$\sqrt { 3 }$
D.$2 - \sqrt { 3 }$
答案:
D
5. 下列运算正确的是(
A.$\sqrt { ( - 2 ) ^ { 2 } } = - 2$
B.$( 2 \sqrt { 3 } ) ^ { 2 } = 6$
C.$\sqrt { 2 } + \sqrt { 3 } = \sqrt { 5 }$
D.$\sqrt { 2 } × \sqrt { 3 } = \sqrt { 6 }$
D
)A.$\sqrt { ( - 2 ) ^ { 2 } } = - 2$
B.$( 2 \sqrt { 3 } ) ^ { 2 } = 6$
C.$\sqrt { 2 } + \sqrt { 3 } = \sqrt { 5 }$
D.$\sqrt { 2 } × \sqrt { 3 } = \sqrt { 6 }$
答案:
D
6. (2024·山东模拟)如图所示,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为(
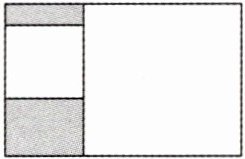
A.$\sqrt { 2 }$
B.2
C.$2 \sqrt { 2 }$
D.6
B
)
A.$\sqrt { 2 }$
B.2
C.$2 \sqrt { 2 }$
D.6
答案:
B
7. (2022·东莞)计算$\sqrt { 8 a } ÷ \sqrt { 2 a }$的结果为(
A.$\sqrt { 2 }$
B.$\sqrt { 6 a }$
C.2
D.$4 a$
C
)A.$\sqrt { 2 }$
B.$\sqrt { 6 a }$
C.2
D.$4 a$
答案:
C
8. (2023·临沂)设$m = 5 \sqrt { \frac { 1 } { 5 } } - \sqrt { 45 }$,则实数$m$所在的范围是(
A.$m < - 5$
B.$- 5 < m < - 4$
C.$- 4 < m < - 3$
D.$m > - 3$
B
)A.$m < - 5$
B.$- 5 < m < - 4$
C.$- 4 < m < - 3$
D.$m > - 3$
答案:
B
9. (河北中考)已知:$\sqrt { 18 } - \sqrt { 2 } = a \sqrt { 2 } - \sqrt { 2 } = b \sqrt { 2 }$,则$ab = $
6
。
答案:
6
10. (2022·衡阳)计算:$\sqrt { 2 } × \sqrt { 8 } = $
4
。
答案:
4
查看更多完整答案,请扫码查看


