《2025年轻松暑假复习加预习中国海洋大学出版社八年级数学54制》

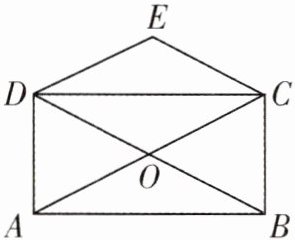
9. 如图,矩形ABCD的对角线AC,BD相交于点O,CE//BD,DE//AC,∠COB= 60°.若四边形CODE的周长为8,则AB的长为(C)



A.4
B.2
C.2√3
D.√3

答案： 9. C

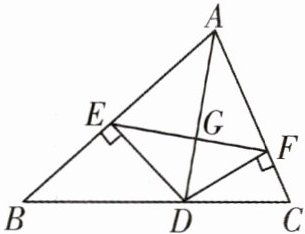
10. 如图所示,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于G.有以下四个结论：①GA= GD ②AD⊥EF ③当∠BAC= 90°时,四边形AEDF是正方形$ ④AE^2+DF^2= AF^2+DE^2.$其中正确的是(D)


A.②③
B.②④
C.①③④
D.②③④

答案： 10. D

11. 已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为$24cm^2.$

答案： 11. 24

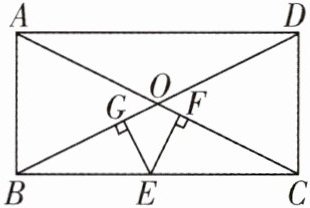
12. (2023·内江)出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建的.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图所示,在矩形ABCD中,AB= 5,AD= 12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG= ______$\frac{60}{13}$.

答案： 12. $\frac{60}{13}$

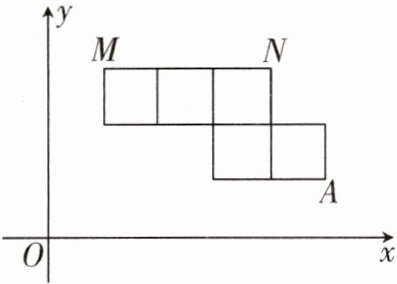
13. (2024·江苏模拟)如图所示,将5个大小相同的正方形置于平面直角坐标系中,若顶点M,N的坐标分别为(3,9),(12,9),则顶点A的坐标为______.

13. $(15,3)$
13. (2024·江苏模拟)如图所示,将5个大小相同的正方形置于平面直角坐标系中,若顶点M,N的坐标分别为(3,9),(12,9),则顶点A的坐标为__$(15,3)$__.

答案： 13. $(15,3)$

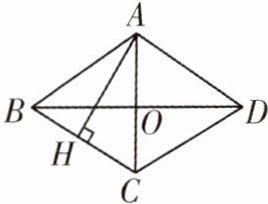
14. (2024·广西模拟)如图所示,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AH⊥BC于点H,已知BO= 4,S_{菱形ABCD}= 24,则AH= ______.

14. $\frac{24}{5}$
填入答案后的题目：
14. (2024·广西模拟)如图所示,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AH⊥BC于点H,已知BO= 4,S_{菱形ABCD}= 24,则AH= ______.

14. $\frac{24}{5}$

答案： 14. $\frac{24}{5}$

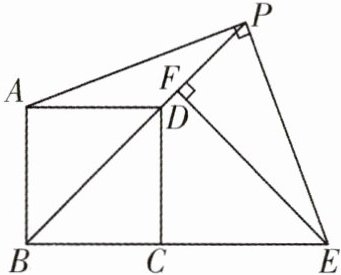
15. (辽宁中考)如图所示,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中：①PA= PE ②CE= √2PD ③BF-PD= 1/2BD ④S_{△PEF}= S_{△ADP}.正确的是______.(填写所有正确结论的序号)

15. ①②③
15. (辽宁中考)如图所示,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中：①PA= PE ②CE= √2PD ③BF-PD= 1/2BD ④S_{△PEF}= S_{△ADP}.正确的是__①②③__.(填写所有正确结论的序号)

答案： 15. ①②③

16. (10分)(2022·长沙)如图,在□ABCD中,对角线AC,BD相交于点O,AB= AD.
(1)求证：AC⊥BD；
证明：∵ 四边形 $ABCD$ 是平行四边形, $AB = AD$,
∴ $□ ABCD$ 是菱形,
∴ $AC \perp BD$;
(2)若点E,F分别为AD,AO的中点,连接EF,EF= 3/2,AO= 2,求BD的长及四边形ABCD的周长.
解：∵ 点 $E,F$ 分别为 $AD,AO$ 的中点,
∴ $EF$ 是 $\triangle AOD$ 的中位线,
∴ $OD = 2EF = 3$,
由 (1) 可知, 四边形 $ABCD$ 是菱形,
∴ $AB = BC = CD = AD,AC \perp BD,BD = 2OD = 6$,
在 $Rt\triangle AOD$ 中, 由勾股定理得 $AD = \sqrt{AO^2 + OD^2} = \sqrt{2^2 + 3^2} = \sqrt{13}$,
∴ 菱形 $ABCD$ 的周长 $= 4AD = 4\sqrt{13}$.

答案： 16. 解:
(1) 证明:
∵ 四边形 $ABCD$ 是平行四边形, $AB = AD$,
∴ $□ ABCD$ 是菱形,
∴ $AC \perp BD$;
(2)
∵ 点 $E,F$ 分别为 $AD,AO$ 的中点,
∴ $EF$ 是 $\triangle AOD$ 的中位线,
∴ $OD = 2EF = 3$,
由
(1) 可知, 四边形 $ABCD$ 是菱形,
∴ $AB = BC = CD = AD,AC \perp BD,BD = 2OD = 6$,
在 $Rt\triangle AOD$ 中, 由勾股定理得 $AD = \sqrt{AO^2 + OD^2} = \sqrt{2^2 + 3^2} = \sqrt{13}$,
∴ 菱形 $ABCD$ 的周长 $= 4AD = 4\sqrt{13}$.