2025年轻松暑假复习加预习中国海洋大学出版社八年级数学54制
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年轻松暑假复习加预习中国海洋大学出版社八年级数学54制 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页

答案:
①邻边相等的 ②都相等 ③互相垂直 ④互相垂直 ⑤四条边 ⑥有一个角是直角 ⑦都是直角 ⑧相等 ⑨对角线相等 ⑩有三个角是直角 ⑪斜边的一半 ⑫这边的一半 ⑬有一组邻边相等的矩形 ⑭直角 ⑮相等 ⑯相等且互相垂直平分 ⑰对角线相等 ⑱对角线垂直 ⑲有一个角是直角
1. 下列结论中,矩形具有而菱形不一定具有的性质是 (
A.内角和为 $ 360 ^ { \circ } $
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
C
)A.内角和为 $ 360 ^ { \circ } $
B.对角线互相平分
C.对角线相等
D.对角线互相垂直
答案:
C
2. (2022·安徽)两个矩形的位置如图所示,若 $ \angle 1 = \alpha $,则 $ \angle 2 = $ (
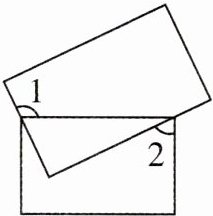
A.$ \alpha - 90 ^ { \circ } $
B.$ \alpha - 45 ^ { \circ } $
C.$ 180 ^ { \circ } - \alpha $
D.$ 270 ^ { \circ } - \alpha $
C
)
A.$ \alpha - 90 ^ { \circ } $
B.$ \alpha - 45 ^ { \circ } $
C.$ 180 ^ { \circ } - \alpha $
D.$ 270 ^ { \circ } - \alpha $
答案:
C
3. (2024·山东模拟)如图所示,在平行四边形 $ A B C D $ 中, $ M $, $ N $ 是 $ B D $ 上两点, $ B M = D N $,连接 $ A M $, $ M C $, $ C N $, $ N A $,添加一个条件,使四边形

$AMCN$是菱形,添加条件可以为$AC\perp BD$(答案不唯一)

答案:
1. 首先,根据平行四边形的性质:
因为四边形$ABCD$是平行四边形,所以$OA = OC$,$OB = OD$。
又因为$BM = DN$,所以$OB−BM = OD - DN$,即$OM = ON$。
2. 然后,根据平行四边形的判定定理(对角线互相平分的四边形是平行四边形):
已知$OA = OC$,$OM = ON$,所以四边形$AMCN$是平行四边形。
若添加条件$AC\perp BD$(答案不唯一):
因为四边形$AMCN$是平行四边形,且$AC\perp MN$($MN$和$BD$共线)。
根据菱形的判定定理(对角线互相垂直的平行四边形是菱形),所以平行四边形$AMCN$是菱形。
故答案可以为$AC\perp BD$(答案不唯一),使四边形$AMCN$是菱形。
因为四边形$ABCD$是平行四边形,所以$OA = OC$,$OB = OD$。
又因为$BM = DN$,所以$OB−BM = OD - DN$,即$OM = ON$。
2. 然后,根据平行四边形的判定定理(对角线互相平分的四边形是平行四边形):
已知$OA = OC$,$OM = ON$,所以四边形$AMCN$是平行四边形。
若添加条件$AC\perp BD$(答案不唯一):
因为四边形$AMCN$是平行四边形,且$AC\perp MN$($MN$和$BD$共线)。
根据菱形的判定定理(对角线互相垂直的平行四边形是菱形),所以平行四边形$AMCN$是菱形。
故答案可以为$AC\perp BD$(答案不唯一),使四边形$AMCN$是菱形。
4. (2023·内蒙古)如图所示,在菱形ABCD中,AB= 4,∠A= 120°,顺次连接菱形ABCD各边中点E,F,G,H,则四边形EFGH的周长为(
A.$4 + 2\sqrt{3}$
B.$6 + 2\sqrt{3}$
C.$4 + 4\sqrt{3}$
D.$6 + 4\sqrt{3}$
C
)
A.$4 + 2\sqrt{3}$
B.$6 + 2\sqrt{3}$
C.$4 + 4\sqrt{3}$
D.$6 + 4\sqrt{3}$
答案:
4.C
查看更多完整答案,请扫码查看


