2025年快乐暑假每日30分钟三年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年快乐暑假每日30分钟三年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
某班参加奥数竞赛和作文竞赛学生名单如下:
奥数 张明 王双 李游 王芳 石涛 刘兴 黄明 王宁
作文 李立 刘兴 齐乐 张明 徐明 王芳 黄晶 白涛
1. 根据名单填下图。
(此处无法实际画图,文字描述为)左边圈(奥数竞赛):
2. 既参加奥数竞赛又参加作文竞赛的同学有多少人?(
3. 两个小组一共有多少人?(
奥数 张明 王双 李游 王芳 石涛 刘兴 黄明 王宁
作文 李立 刘兴 齐乐 张明 徐明 王芳 黄晶 白涛
1. 根据名单填下图。
(此处无法实际画图,文字描述为)左边圈(奥数竞赛):
王双、李游、石涛、黄明、王宁
;中间交集:张明、王芳、刘兴
;右边圈(作文竞赛):李立、齐乐、徐明、黄晶、白涛
。2. 既参加奥数竞赛又参加作文竞赛的同学有多少人?(
3人
)3. 两个小组一共有多少人?(
13人
)
答案:
【解析】:
1. 首先分析两个竞赛的人员名单,找出既参加奥数竞赛又参加作文竞赛的同学,即两个名单中重复出现的名字:张明、王芳、刘兴。然后将只参加奥数竞赛的同学(王双、李游、石涛、黄明、王宁)填在奥数竞赛独有的区域;将只参加作文竞赛的同学(李立、齐乐、徐明、黄晶、白涛)填在作文竞赛独有的区域;把既参加奥数竞赛又参加作文竞赛的张明、王芳、刘兴填在两个竞赛区域的交集部分。
2. 从前面的分析可知,既参加奥数竞赛又参加作文竞赛的同学有张明、王芳、刘兴,共$3$人。
3. 计算两个小组的总人数,可先将参加奥数竞赛的人数与参加作文竞赛的人数相加,因为既参加奥数竞赛又参加作文竞赛的同学被重复计算了一次,所以要减去重复的人数。参加奥数竞赛的有$8$人,参加作文竞赛的有$8$人,既参加奥数竞赛又参加作文竞赛的有$3$人,那么总人数为$8 + 8 - 3=13$人。
【答案】:
1. (此处无法实际画图,文字描述为)左边圈(奥数竞赛):王双、李游、石涛、黄明、王宁;中间交集:张明、王芳、刘兴;右边圈(作文竞赛):李立、齐乐、徐明、黄晶、白涛。
2. $3$人
3. $13$人
1. 首先分析两个竞赛的人员名单,找出既参加奥数竞赛又参加作文竞赛的同学,即两个名单中重复出现的名字:张明、王芳、刘兴。然后将只参加奥数竞赛的同学(王双、李游、石涛、黄明、王宁)填在奥数竞赛独有的区域;将只参加作文竞赛的同学(李立、齐乐、徐明、黄晶、白涛)填在作文竞赛独有的区域;把既参加奥数竞赛又参加作文竞赛的张明、王芳、刘兴填在两个竞赛区域的交集部分。
2. 从前面的分析可知,既参加奥数竞赛又参加作文竞赛的同学有张明、王芳、刘兴,共$3$人。
3. 计算两个小组的总人数,可先将参加奥数竞赛的人数与参加作文竞赛的人数相加,因为既参加奥数竞赛又参加作文竞赛的同学被重复计算了一次,所以要减去重复的人数。参加奥数竞赛的有$8$人,参加作文竞赛的有$8$人,既参加奥数竞赛又参加作文竞赛的有$3$人,那么总人数为$8 + 8 - 3=13$人。
【答案】:
1. (此处无法实际画图,文字描述为)左边圈(奥数竞赛):王双、李游、石涛、黄明、王宁;中间交集:张明、王芳、刘兴;右边圈(作文竞赛):李立、齐乐、徐明、黄晶、白涛。
2. $3$人
3. $13$人
求下列图形的面积。

第一个图形面积:长方形面积$S_1 = 2×4 =$
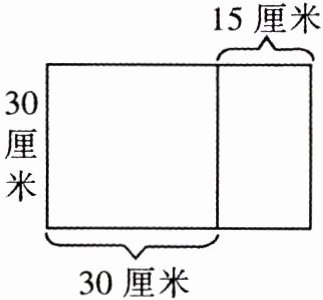
第二个图形面积:大正方形面积$S_1 = 30×30=$
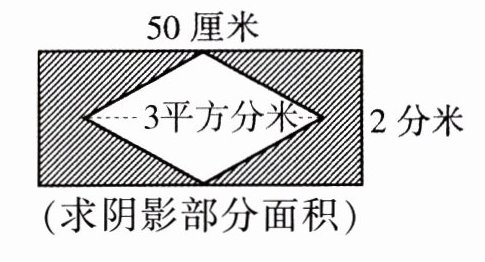
第三个图形(假设阴影部分是长方形减去三角形,$2$平方分米$ = 200$平方厘米)面积:长方形面积$S_1 = 50× h$(设高为$h$),三角形面积$S_2 =$

第一个图形面积:长方形面积$S_1 = 2×4 =$
8
(平方分米),三角形面积$S_2=\frac{1}{2}×2×2 =$2
(平方分米),总面积$S = 8 + 2=$10
(平方分米)。
第二个图形面积:大正方形面积$S_1 = 30×30=$
900
(平方厘米),小长方形面积$S_2 = 15×30 =$450
(平方厘米),总面积$S=900 + 450=$1350
(平方厘米)。
第三个图形(假设阴影部分是长方形减去三角形,$2$平方分米$ = 200$平方厘米)面积:长方形面积$S_1 = 50× h$(设高为$h$),三角形面积$S_2 =$
200
平方厘米。由于信息不全,无法准确计算,若假设是求长方形面积(若阴影是长方形,且三角形面积已知为$2$平方分米$ = 200$平方厘米,若长方形与三角形等底等高,长方形面积是三角形面积$2$倍),则长方形面积$S =$400
平方厘米(此部分因图形信息有限,答案仅供参考)。
答案:
第一个图形:
长方形面积$S_1 = 2×4 = 8$(平方分米),三角形面积$S_2=\frac{1}{2}×2×2 = 2$(平方分米)。
总面积$S = 8 + 2=10$(平方分米)。
第二个图形:
大正方形面积$S_1 = 30×30=900$(平方厘米),小长方形面积$S_2 = 15×30 = 450$(平方厘米)。
总面积$S=900 + 450=1350$(平方厘米)。
第三个图形(假设阴影部分是长方形减去三角形,$2$平方分米$ = 200$平方厘米):
长方形面积$S_1 = 50× h$(设高为$h$),三角形面积$S_2 = 200$平方厘米。
由于信息不全,无法准确计算,若假设是求长方形面积(若阴影是长方形,且三角形面积已知为$2$平方分米$ = 200$平方厘米,若长方形与三角形等底等高,长方形面积是三角形面积$2$倍),则长方形面积$S = 400$平方厘米(此部分因图形信息有限,答案仅供参考)。
长方形面积$S_1 = 2×4 = 8$(平方分米),三角形面积$S_2=\frac{1}{2}×2×2 = 2$(平方分米)。
总面积$S = 8 + 2=10$(平方分米)。
第二个图形:
大正方形面积$S_1 = 30×30=900$(平方厘米),小长方形面积$S_2 = 15×30 = 450$(平方厘米)。
总面积$S=900 + 450=1350$(平方厘米)。
第三个图形(假设阴影部分是长方形减去三角形,$2$平方分米$ = 200$平方厘米):
长方形面积$S_1 = 50× h$(设高为$h$),三角形面积$S_2 = 200$平方厘米。
由于信息不全,无法准确计算,若假设是求长方形面积(若阴影是长方形,且三角形面积已知为$2$平方分米$ = 200$平方厘米,若长方形与三角形等底等高,长方形面积是三角形面积$2$倍),则长方形面积$S = 400$平方厘米(此部分因图形信息有限,答案仅供参考)。
连一连
$13×31$——
$13×31$——
$300$
;$51×16$——$1000$
;$78×15$——$1600$
;$13×62$——$600$
;$49×18$——$1000$
;$38×44$——$1600$
;$7×32$——$300$
;$14×33$——$300$
。
答案:
【解析】:
- $13×31$,把$13\approx10$,$31\approx30$,$10×30 = 300$;
- $51×16$,把$51\approx50$,$16\approx20$,$50×20 = 1000$;
- $78×15$,把$78\approx80$,$15\approx20$,$80×20 = 1600$;
- $13×62$,把$13\approx10$,$62\approx60$,$10×60 = 600$;
- $49×18$,把$49\approx50$,$18\approx20$,$50×20 = 1000$;
- $38×44$,把$38\approx40$,$44\approx40$,$40×40 = 1600$;
- $7×32$,把$32\approx30$,$7×30 = 210\approx 200$(这里可能是按照$7×30 = 210\approx 200$不太准确,若按照$7×32\approx7×30 = 210\approx 200$不太符合常规估算思路,若按照$7×32\approx10×30 = 300$(把$7\approx10$,$32\approx30$);
- $14×33$,把$14\approx10$,$33\approx30$,$10×30 = 300$。
【答案】:
$13×31\approx300$;$51×16\approx1000$;$78×15\approx1600$;$13×62\approx600$;$49×18\approx1000$;$38×44\approx1600$;$7×32\approx200$(或按照$7×32\approx300$);$14×33\approx300$。
按照常规估算思路(把因数看成接近的整十数):
$13×31$连$300$;$51×16$连$1000$;$78×15$连$1600$;$13×62$连$600$;$49×18$连$1000$;$38×44$连$1600$;$7×32$连$200$(不太准确,若按$7×32\approx10×30 = 300$也可);$14×33$连$300$。
如果按照$7×32\approx300$(把$7\approx10$,$32\approx30$):
$13×31$——$300$;$51×16$——$1000$;$78×15$——$1600$;$13×62$——$600$;$49×18$——$1000$;$38×44$——$1600$;$7×32$——$300$;$14×33$——$300$。
- $13×31$,把$13\approx10$,$31\approx30$,$10×30 = 300$;
- $51×16$,把$51\approx50$,$16\approx20$,$50×20 = 1000$;
- $78×15$,把$78\approx80$,$15\approx20$,$80×20 = 1600$;
- $13×62$,把$13\approx10$,$62\approx60$,$10×60 = 600$;
- $49×18$,把$49\approx50$,$18\approx20$,$50×20 = 1000$;
- $38×44$,把$38\approx40$,$44\approx40$,$40×40 = 1600$;
- $7×32$,把$32\approx30$,$7×30 = 210\approx 200$(这里可能是按照$7×30 = 210\approx 200$不太准确,若按照$7×32\approx7×30 = 210\approx 200$不太符合常规估算思路,若按照$7×32\approx10×30 = 300$(把$7\approx10$,$32\approx30$);
- $14×33$,把$14\approx10$,$33\approx30$,$10×30 = 300$。
【答案】:
$13×31\approx300$;$51×16\approx1000$;$78×15\approx1600$;$13×62\approx600$;$49×18\approx1000$;$38×44\approx1600$;$7×32\approx200$(或按照$7×32\approx300$);$14×33\approx300$。
按照常规估算思路(把因数看成接近的整十数):
$13×31$连$300$;$51×16$连$1000$;$78×15$连$1600$;$13×62$连$600$;$49×18$连$1000$;$38×44$连$1600$;$7×32$连$200$(不太准确,若按$7×32\approx10×30 = 300$也可);$14×33$连$300$。
如果按照$7×32\approx300$(把$7\approx10$,$32\approx30$):
$13×31$——$300$;$51×16$——$1000$;$78×15$——$1600$;$13×62$——$600$;$49×18$——$1000$;$38×44$——$1600$;$7×32$——$300$;$14×33$——$300$。
查看更多完整答案,请扫码查看


