1. 当杠杆在动力和阻力的作用下
静止
时,我们就说此时杠杆处于平衡状态。
答案:
静止
2. 杠杆的平衡条件是
动力×动力臂=阻力×阻力臂
,用字母表示可写成$F_{1}l_{1}=F_{2}l_{2}$
。杠杆的平衡条件也称为杠杆原理
。
答案:
动力×动力臂=阻力×阻力臂 $F_{1}l_{1}=F_{2}l_{2}$ 杠杆原理
1. 探究杠杆的平衡条件:
(1) 小王把杠杆放在支架上后,在如图甲所示的位置静止,此时杠杆处于
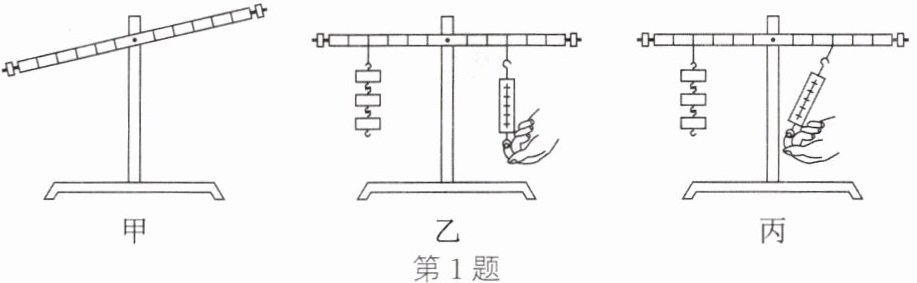
(2) 如图乙所示,在右边用弹簧测力计竖直向下拉,使杠杆在水平位置平衡时,左边钩码离支点20cm,右边挂钩离支点15cm,每个钩码重为1N,则此时弹簧测力计示数应为
(3) 如图丙所示,当杠杆在水平位置平衡时,与图乙相比弹簧测力计示数将
(4) 在实验中,多次改变力和力臂的大小主要是为了
A. 减小摩擦
B. 获取多组实验数据,归纳出物理规律
C. 多次测量取平均值减小误差
D. 使每组数据更准确
(1) 小王把杠杆放在支架上后,在如图甲所示的位置静止,此时杠杆处于
平衡
(平衡/不平衡)状态。为了将杠杆调至水平位置平衡,他应将右端的平衡螺母向右
(左/右)调节。当杠杆在水平位置平衡时,杠杆自重的力臂为0
cm。实验中使杠杆在水平位置平衡的好处是消除杠杆自重对实验的影响,且便于测量力臂
。
(2) 如图乙所示,在右边用弹簧测力计竖直向下拉,使杠杆在水平位置平衡时,左边钩码离支点20cm,右边挂钩离支点15cm,每个钩码重为1N,则此时弹簧测力计示数应为
4
N。(3) 如图丙所示,当杠杆在水平位置平衡时,与图乙相比弹簧测力计示数将
变大
(变大/不变/变小),这是因为弹簧测力计拉力的力臂变短了
(变长了/不变/变短了)。(4) 在实验中,多次改变力和力臂的大小主要是为了
B
。A. 减小摩擦
B. 获取多组实验数据,归纳出物理规律
C. 多次测量取平均值减小误差
D. 使每组数据更准确
答案:
(1)平衡 右 0 消除杠杆自重对实验的影响,且便于测量力臂
(2)4
(3)变大 变短了
(4)B
(1)平衡 右 0 消除杠杆自重对实验的影响,且便于测量力臂
(2)4
(3)变大 变短了
(4)B
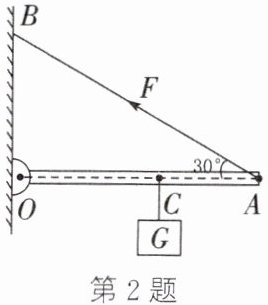
2. 如图所示,一轻质杠杆OA可绕O点无摩擦转动,A端用绳子系在竖直墙壁的B点,在杠杆的C点悬挂一重为20N的物体,杠杆处于水平静止状态。已知OA长50cm,OC长30cm,∠OAB= 30°。
(1) 请在图中画出绳子对杠杆的拉力F的力臂$l_{1}$。
(2) 拉力F的大小是多少?
(1) 请在图中画出绳子对杠杆的拉力F的力臂$l_{1}$。
(2) 拉力F的大小是多少?

答案:
(1)如图所示
(2)如图所示,在Rt△ODA中,∠OAD = 30°,则$OD=\frac{1}{2}OA=\frac{1}{2}×50\,\text{cm}=25\,\text{cm}$,根据杠杆的平衡条件得,$F× l_{1}=G× OC$,即$F = G×\frac{OC}{l_{1}}=20\,\text{N}×\frac{30\,\text{cm}}{25\,\text{cm}}=24\,\text{N}$
(1)如图所示
(2)如图所示,在Rt△ODA中,∠OAD = 30°,则$OD=\frac{1}{2}OA=\frac{1}{2}×50\,\text{cm}=25\,\text{cm}$,根据杠杆的平衡条件得,$F× l_{1}=G× OC$,即$F = G×\frac{OC}{l_{1}}=20\,\text{N}×\frac{30\,\text{cm}}{25\,\text{cm}}=24\,\text{N}$

查看更多完整答案,请扫码查看


