《2025年通城学典课时作业本九年级物理上册苏科版苏州专版》

1. 机械效率计算公式：$\eta =$$\frac{W_{有用}}{W_{总}} × 100\%$。

答案： $\frac{W_{有用}}{W_{总}} × 100\%$

2. 滑轮组(竖直方向匀速提升物体)的机械效率：
(1)已知物重$G$、拉力$F$、物体上升的高度$h$、自由端移动的距离$s$,则机械效率$\eta =$$\frac{Gh}{Fs} × 100\%$。
(2)已知物重$G$、拉力$F$、绳子的段数$n$,则机械效率$\eta =$$\frac{G}{nF} × 100\%$。
(3)已知物重$G$、动滑轮重$G_{动}$、不计绳重和摩擦,则机械效率$\eta =$$\frac{G}{G+G_{动}} × 100\%$。

答案： （1）$\frac{Gh}{Fs} × 100\%$ （2）$\frac{G}{nF} × 100\%$ （3）$\frac{G}{G+G_{动}} × 100\%$

3. 斜面的机械效率：
(1)已知物重$G$、斜面的高度$h$、斜面的长度$s$、拉力$F$,则机械效率$\eta =$$\frac{Gh}{Fs} × 100\%$。
(2)已知物重$G$、斜面的高度$h$、斜面的长度$s$、摩擦力$f$,则机械效率$\eta =$$\frac{Gh}{Gh+fs} × 100\%$。
(3)已知斜面的长度$s$、摩擦力$f$、拉力$F$,则机械效率$\eta =$$(1-\frac{f}{F}) × 100\%$。

答案： （1）$\frac{Gh}{Fs} × 100\%$ （2）$\frac{Gh}{Gh+fs} × 100\%$ （3）$(1-\frac{f}{F}) × 100\%$

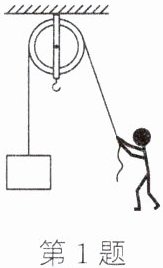
1. (2024·南通)如图,工人用$330N$的拉力,使用定滑轮将质量为$30kg的物体在6s内匀速吊起3m$,$g取10N/kg$。求：
(1)物体上升的速度。
(2)工人做功的功率。
(3)定滑轮的机械效率。(结果精确到$0.1\%$)

答案： （1）物体上升的速度$v=\frac{h}{t}=\frac{3\ \text{m}}{6\ \text{s}}=0.5\ \text{m/s}$ （2）拉力端移动距离$s=h=3\ \text{m}$,拉力做的总功$W_{总}=Fs=330\ \text{N} × 3\ \text{m}=990\ \text{J}$;拉力做功功率即工人做功的功率$P=\frac{W_{总}}{t}=\frac{990\ \text{J}}{6\ \text{s}}=165\ \text{W}$ （3）物体重力$G=mg=30\ \text{kg} × 10\ \text{N/kg}=300\ \text{N}$,克服物体重力做的有用功$W_{有用}=Gh=300\ \text{N} × 3\ \text{m}=900\ \text{J}$,定滑轮的机械效率$\eta=\frac{W_{有用}}{W_{总}} × 100\%=\frac{900\ \text{J}}{990\ \text{J}} × 100\% \approx 90.9\%$

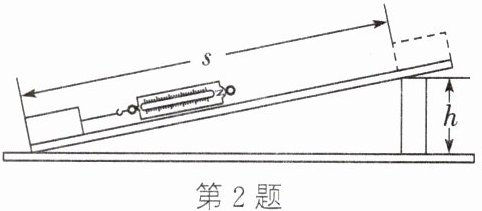
2. 如图所示,斜面长为$5m$,高为$1m$,把重为$5000N$的物体匀速地拉向斜面顶端,此时斜面的机械效率为$80\%$,则：
(1)有用功是多少？
(2)所用拉力为多少？
(3)物体受到的摩擦力为多少？

答案： （1）有用功$W_{有用}=Gh=5000\ \text{N} × 1\ \text{m}=5000\ \text{J}$ （2）由$\eta=\frac{W_{有用}}{W_{总}} × 100\%$得,总功$W_{总}=\frac{W_{有用}}{\eta}=\frac{5000\ \text{J}}{80\%}=6250\ \text{J}$;由$W_{总}=Fs$得,拉力$F=\frac{W_{总}}{s}=\frac{6250\ \text{J}}{5\ \text{m}}=1250\ \text{N}$ （3）此过程的额外功$W_{额外}=W_{总}-W_{有用}=6250\ \text{J}-5000\ \text{J}=1250\ \text{J}$;由$W_{额外}=fs$得,摩擦力$f=\frac{W_{额外}}{s}=\frac{1250\ \text{J}}{5\ \text{m}}=250\ \text{N}$