《2025年经纶学典提高班一年级数学上册苏教版》

例1 中国古代算筹。

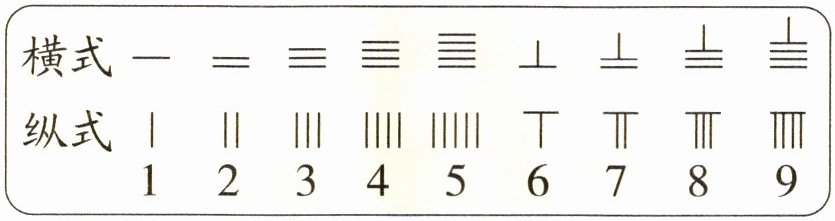
中国古代算筹有横式和纵式两种,你能说说算筹表示数字的规律吗?
💡我的思考
首先整体观察横式和纵式,发现相同的数字算筹数量相同,只是算筹的(方向)不同,但是记数思想是相同的,因此我们单独探索横式的规律,纵式在横式的规律上换个(方向)即可。
💡规律探究
可以发现横式中有(—)和(|)两种算筹。观察1~5可以发现算筹的种类相同,但是数量不同,通过计算发现运用了(加)法。再根据1~5的规律观察6~9,同样也可以用(加)法算出,其中|表示(5)。
因此可以总结算筹表示数的规律:有2种不同的基础算筹,然后通过两种算筹互相之间(相加),即可表示出数。横式和纵式的表达方法相同,只是算筹的(方向)不同。

答案： 我的思考
方向 方向
规律探究
— | 加 加 5 相加 方向