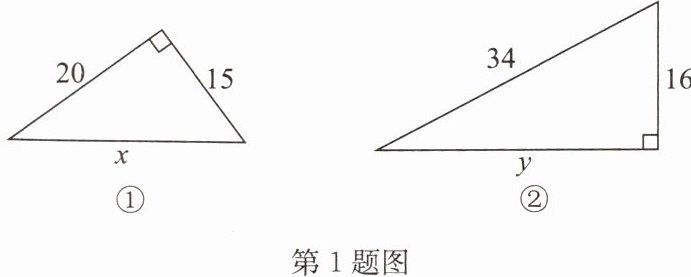
1. 如图,求直角三角形中未知边的长度.

答案:
解:题图①中,由勾股定理,得$x^{2}=20^{2}+15^{2}$,解得$x=\pm 25$.
∵x表示边长,
∴x=25.题图②中,由勾股定理,得$y^{2}=34^{2}-16^{2}$,解得$y=\pm 30$.
∵y表示边长,
∴y=30.
∵x表示边长,
∴x=25.题图②中,由勾股定理,得$y^{2}=34^{2}-16^{2}$,解得$y=\pm 30$.
∵y表示边长,
∴y=30.
2. 根据所给条件,解决下列问题:
求:(1)图①中BC的长;
(2)图②中BC的长.
求:(1)图①中BC的长;
(2)图②中BC的长.

答案:
解:
(1)
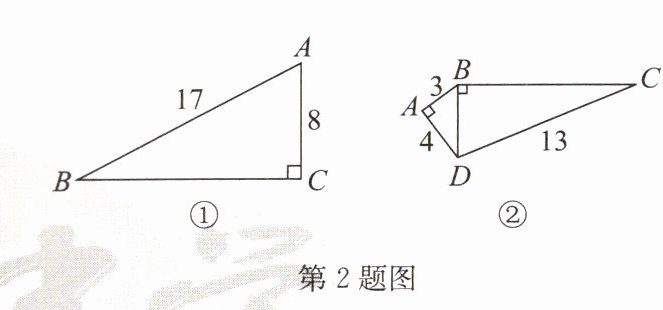
∵$BC^{2}=AB^{2}-AC^{2}=17^{2}-8^{2}=225$,
∴BC=15.
(2)
∵$BD^{2}=AB^{2}+AD^{2}=3^{2}+4^{2}=25$,
∴$BC^{2}=CD^{2}-BD^{2}=13^{2}-25=144$,
∴BC=12.
(1)
∵$BC^{2}=AB^{2}-AC^{2}=17^{2}-8^{2}=225$,
∴BC=15.
(2)
∵$BD^{2}=AB^{2}+AD^{2}=3^{2}+4^{2}=25$,
∴$BC^{2}=CD^{2}-BD^{2}=13^{2}-25=144$,
∴BC=12.
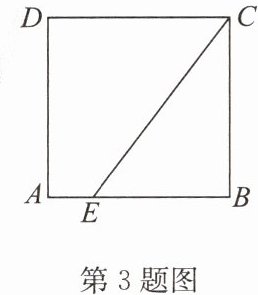
3. 如图,点E在正方形ABCD的边AB上,若$BE= 6$,$CE= 10$,求正方形ABCD的面积.

答案:
解:
∵四边形ABCD是正方形,
∴∠B=90°.在Rt△BCE中,由勾股定理,得$BC^{2}=CE^{2}-BE^{2}=10^{2}-6^{2}=64$,
∴正方形ABCD的面积为$BC^{2}=64$.
∵四边形ABCD是正方形,
∴∠B=90°.在Rt△BCE中,由勾股定理,得$BC^{2}=CE^{2}-BE^{2}=10^{2}-6^{2}=64$,
∴正方形ABCD的面积为$BC^{2}=64$.
4. 如图,在$Rt\triangle ABC$中,$\angle C= 90^{\circ}$,AB的垂直平分线分别交AB,AC于点D,E. 若$AC= 8$,$BC= 4$,求AE的长.


答案:
解:连接BE,如答图.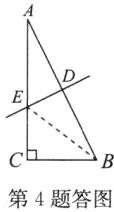
∵DE垂直平分AB,
∴AE=BE.设AE=BE=x,则CE=8−x.在Rt△BCE中,$BC^{2}+CE^{2}=BE^{2}$,
∴$4^{2}+(8 - x)^{2}=x^{2}$,解得x=5,
∴AE=5.
解:连接BE,如答图.

∵DE垂直平分AB,
∴AE=BE.设AE=BE=x,则CE=8−x.在Rt△BCE中,$BC^{2}+CE^{2}=BE^{2}$,
∴$4^{2}+(8 - x)^{2}=x^{2}$,解得x=5,
∴AE=5.
查看更多完整答案,请扫码查看


