《2025年精彩三年就练这一本八年级数学上册浙教版》

1. 下列各式中,是不等式的是 ( )

A.$x= 3$
B.$x-1＞0$
C.$x+y= 1$
D.$4x+5$

答案： B

2. 如图,该数轴表示的不等式的范围为 ( )


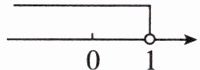
A.$x\leq1$
B.$x＜1$
C.$x\geq1$
D.$x＞1$

答案： B

3. 若$a＞b$,则$ac＜bc$成立,那么 ( )

A.$c＞0$
B.$c\geq0$
C.$c＜0$
D.$c\leq0$

答案： C

4. 如图,这是一个运行程序,规定:从“输入一个值$x$”到“结果是否$＞26$”为一次程序操作,如果程序操作进行了1次后就停止,则$x$的最小整数值为 ( )


A.7
B.8
C.9
D.10

答案： D

5. 把不等式组$\begin{cases} x+1\geq2 \\ -2x-3\geq-9 \end{cases} $的解集用数轴上的点表示出来,则其解构成的图形为 ( )

A.射线
B.线段
C.直线
D.长方形

答案： B

6. 规定$\max\{m,n\}(m\neq n)表示m,n$中较大的数,若$\max\left\{ \frac{x-3}{2}-\frac{2x-1}{3},1 \right\}=1$,则$x$的取值范围是 ( )

A.$x＜-13$
B.$x＞-13$
C.$x＞-17$
D.$x＜-17$

答案： B

7. 若不等式$3(x+1)-2\leq4(x-3)+1的最小整数解是方程\frac{1}{2}x-m= 5$的解,则$m$的值为 ( )

A.1
B.$-11$
C.$\frac{3}{2}$
D.$-\frac{23}{2}$

答案： A

8. 某单位需要购买分类垃圾桶8个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶50元/个,B型分类垃圾桶55元/个,总费用不超过415元,则不同的购买方式有 ( )

A.2种
B.3种
C.4种
D.5种

答案： C

9. 如图,则$x$ ______ 70。

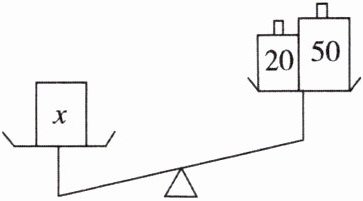
答案： ＞

10. 在$-2,-1,0,1,2$这五个数中,是不等式$2x+3＞0$的解的共有 ______ 个。

答案： 4

11. 已知$x满足2(x-3)\leq x-2$,则$x$的最大值为 ______。

答案： 4

12. 已知$x\geq2的最小值是a$,$x\leq-6的最大值是b$,则$a+b= $ ______。

答案： -4

13. 若关于$x的不等式组\begin{cases} 2x - b \geq 0 \\ x + a \leq 0 \end{cases} 的解集为3\leq x\leq4$,则关于$x的不等式ax + b ＜ 0$的解集为 ______。

答案： $x＞\frac{3}{2}$

14. (8分)小张同学解不等式$\frac{x+3}{5}\leq\frac{2x-5}{3}-1$时出现了错误,解答过程如下:
去分母,得$3(x+3)\leq5(2x-5)-1$。(第一步)
去括号,得$3x+9\leq10x-25-1$。(第二步)
移项,合并同类项,得$-7x\leq-35$。(第三步)
解得$x\geq5$。(第四步)
(1)小张同学的解答过程是从第 ______ 步开始出错的,出错的原因是 ______。
(2)请写出此题正确的解答过程。

答案：
(1)小张同学解答过程是从第一步开始出错的，出错的原因是-1未乘15，故答案为一；-1未乘15。
(2)$\frac{x+3}{5}\leqslant\frac{2x-5}{3}-1$，
去分母得，$3(x+3)\leqslant5(2x-5)-15$，
去括号得，$3x+9\leqslant10x-25-15$，
移项、合并同类项得，$-7x\leqslant -49$，
系数化为1得，$x\geqslant 7$。