《2025年精彩三年就练这一本八年级数学上册浙教版》

1. 下列四个图形中,是轴对称图形的是 ( )

A.
B.
C.
D.

答案： D

2. 等腰三角形的底角等于50°,则这个等腰三角形顶角的度数是 ( )

A.50°
B.65°
C.80°
D.100°

答案： C

3. 如图,在Rt△ABC中,∠ABC= 90°,∠A= 60°,AB= 7 cm,D是AC的中点,则BD的长为 ( )


A.7.5 cm
B.7 cm
C.6.5 cm
D.6 cm

答案： B

4. 在等腰三角形ABC中,AB= AC,∠A= 70°,则∠B的度数 ( )

A.40°
B.55°
C.60°
D.70°

答案： B

5. 等腰三角形三边长分别为6 cm,5 cm,5 cm,则它的底边上的中线长为 ( )

A.3 cm
B.4 cm
C.5 cm
D.6 cm

答案： B

6. 如图,在等腰三角形ABC中,AD是底边BC上的中线,DE是△ABD的高线.图中与∠BAD一定相等的角有(不含本身) ( )


A.1个
B.2个
C.3个
D.4个

答案： B

7. 如图,在△ABC中,AB= AC,∠BAD= 30°,且AE= AD,则∠EDC= ( )


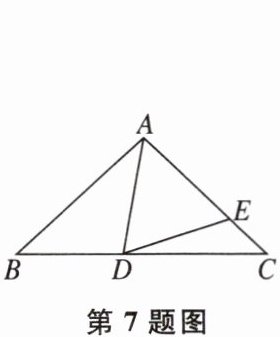
A.7.5°
B.10°
C.12.5°
D.15°

答案： D 【解析】设∠EDC=x,∠B=∠C=y,则∠AED=∠EDC+∠C=x+y。又因为AD=AE,所以∠ADE=∠AED=x+y,则∠ADC=∠ADE+∠EDC=2x+y。又因为∠ADC=∠B+∠BAD,所以2x+y=y+30°,解得x=15°,所以∠EDC的度数是15°。

8. 如图,在Rt△ABC中,∠B= 90°,CD,AE是中线,$CD= \sqrt{40}$,$AC= \sqrt{52}$,则AE的长为 ( )


A.$\sqrt{26}$
B.5
C.6
D.4

答案： B

9. 如图,已知△ABC是等边三角形,则它的外角∠ACD= _°。

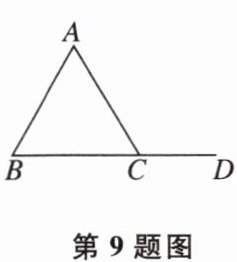
答案： 120

10. 命题“如果ab= 0,那么a= 0,b= 0”的逆命题是_；这个逆命题是_命题。(填“真”或“假”)

答案： 如果a=0,b=0,那么ab=0 真

11. 如图,在Rt△ABC中,∠ACB= 90°,CD⊥AB,∠A= 55°,则∠DCB= _°。

答案： 55°

12. 如图,在△ABC中,AB= AC,AD为△BAC的角平分线,且AD= 4,若△ABD的周长为12,则△ABC的周长是 _。

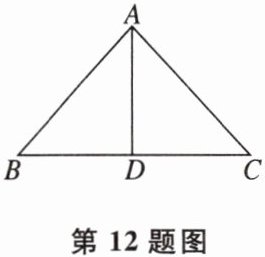
答案： 16

13. 如图,在等腰直角三角形ABC中,AC= BC,D为△ABC内一点,且∠BCD= ∠CAD,若CD= 4,则△BCD的面积为 _。

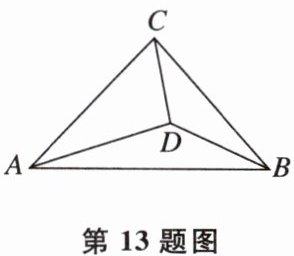
答案：
8 【解析】如图,过点B作BH⊥CD,交CD的延长线于H。 因为在等腰直角三角形ABC中,AC=BC,所以∠ACB=90°。因为∠BCD=∠CAD,所以∠ACB=∠BCD+∠ACD=∠CAD+∠ACD=90°,所以∠ADC=90°,所以∠ACB=∠ADC=∠H=90°。在△ACD和△CBH中,{∠CAD=∠BCD,∠ADC=∠H,AC=CB}所以△ACD≌△CBH(AAS),所以BH=CD=4,所以S△BCD=$\frac{1}{2}$CD·BH=$\frac{1}{2}$×4×4=8。