《2025年全效学习九年级数学上下册浙教版》

1. 如图,在△ABC中,点D在AB上,下列条件中,能使△CBD和△ABC相似的是(D)

A.∠ACD= ∠B
B.∠ADC= ∠ACB
C.$AC^{2}= AD\cdot AB$
D.$BC^{2}= BD\cdot BA$

答案： D

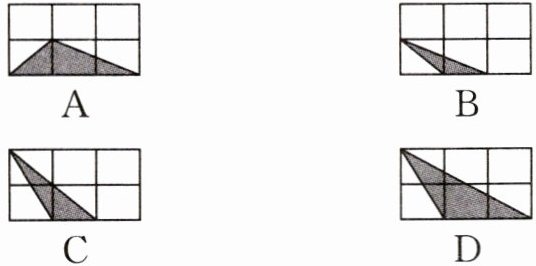
2. 如图的图形及各个选项均是由边长为1的小正方形组成的网格,三角形的顶点均在小正方形的顶点上,则阴影部分与△ABC相似的是(B)


 

答案： B

3. 如图,在梯形ABCD中,AD//BC,点F,E分别在线段BC,AC上,且∠FAC= ∠ADE,AC= AD.
(1)求证：DE= AF.
(2)若∠ABC= ∠CDE,求证：$AF^{2}= BF\cdot CE$.

答案：
(1)证明：
∵AD//BC，
∴∠DAC=∠ACB（两直线平行，内错角相等）。
在△ADE和△CAF中，
∠ADE=∠CAF（已知），
AD=CA（已知AC=AD），
∠DAE=∠ACF（
∵∠DAC=∠ACB，即∠DAE=∠ACF），
∴△ADE≌△CAF（ASA），
∴DE=AF。
(2)证明：
∵△ADE≌△CAF，
∴∠AED=∠CFA。
∵∠AED+∠DEC=180°，∠CFA+∠AFB=180°，
∴∠DEC=∠AFB（等角的补角相等）。
在△ABF和△CDE中，
∠ABF=∠CDE（已知），
∠AFB=∠DEC（已证），
∴△ABF∽△CDE（AA）。
∴BF/DE=AF/CE（相似三角形对应边成比例）。
∵DE=AF（已证），
∴BF/AF=AF/CE，
∴AF²=BF·CE。

4. 如图,在菱形ABCD中,点G在边CD上,连结AG并延长,交BC的延长线于点F,连结BD,交AF于点E,连结CE.
(1)若BE= BC,∠ABC= 80°,求∠DAE的度数.
(2)求证：$EC^{2}= EF\cdot EG$.
(3)若AB= 6,$\frac{CE}{EG}= 3$,求CF的长.

答案： 1. （1）
因为四边形$ABCD$是菱形，所以$AB = AD$，$∠ABD=∠CBD=\frac{1}{2}∠ABC$。
已知$∠ABC = 80^{\circ}$，则$∠ABD = ∠CBD=\frac{1}{2}×80^{\circ}=40^{\circ}$。
又因为$BE = BC$，所以$∠BEC=∠BCE$。
根据三角形内角和定理，$∠BEC=\frac{1}{2}(180^{\circ}-∠CBD)=\frac{1}{2}(180 - 40)^{\circ}=70^{\circ}$。
因为$AD// BC$，所以$∠DAE = ∠F$。
又因为$∠BEC$是$\triangle ECF$的外角，$∠BEC = ∠F+∠ECF$，且$∠ECF = ∠BCA$，$∠BCA=∠DAC$（菱形的性质：$AD// BC$，$AC$平分$∠BAD$）。
因为$∠DAE = ∠F$，$∠BEC = 70^{\circ}$，$∠ECF = ∠DAE$，所以$∠DAE=\frac{1}{2}∠BEC = 30^{\circ}$。
2. （2）
证明：
因为四边形$ABCD$是菱形，所以$AD = CD$，$∠ADE = ∠CDE$，$AD// BC$。
在$\triangle ADE$和$\triangle CDE$中，$\begin{cases}AD = CD\\∠ADE = ∠CDE\\DE = DE\end{cases}$，根据$SAS$（边角边）定理可得$\triangle ADE\cong\triangle CDE$。
所以$∠DAE = ∠DCE$。
因为$AD// BC$，所以$∠DAE = ∠F$，则$∠DCE = ∠F$。
又因为$∠CEG = ∠FEC$（公共角）。
所以$\triangle CEG\sim\triangle FEC$（两角分别相等的两个三角形相似）。
根据相似三角形的性质：$\frac{EC}{EF}=\frac{EG}{EC}$，即$EC^{2}=EF\cdot EG$。
3. （3）
因为$\frac{CE}{EG}=3$，设$EG = x$，则$CE = 3x$。
由$EC^{2}=EF\cdot EG$，可得$(3x)^{2}=EF\cdot x$，所以$EF = 9x$。
因为$AD// BC$，所以$\triangle ADG\sim\triangle FCG$。
则$\frac{AD}{CF}=\frac{AG}{GF}$。
又因为$\triangle ADE\cong\triangle CDE$，所以$AE = CE = 3x$。
$AG=AE + EG=3x + x=4x$，$GF=EF - EG=9x - x = 8x$。
已知$AD = AB = 6$，由$\frac{AD}{CF}=\frac{AG}{GF}$，即$\frac{6}{CF}=\frac{4x}{8x}$。
化简$\frac{4x}{8x}=\frac{1}{2}$，则$\frac{6}{CF}=\frac{1}{2}$，解得$CF = 12$。
综上，（1）$∠DAE = 30^{\circ}$；（2）证明过程如上述；（3）$CF = 12$。

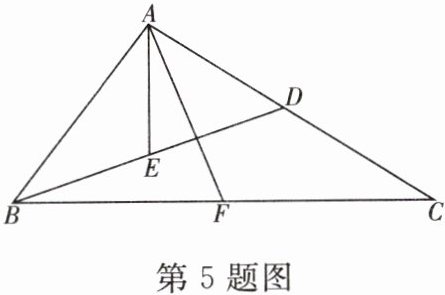
5. 如图,在△ABC中,点D,E,F分别在线段AC,BD,BC上.从下列条件中选择其中两个：①$AB^{2}= AD\cdot AC$；②∠BAE= ∠CAF；③$\frac{AB}{AC}= \frac{BE}{CF}$,完成如下的证明.
(1)求证：△ABE∽△ACF.
(2)连结EF,如果BF= CF,求证：EF//AC.

答案：
(1)选择条件①和②。
证明：
∵AB²=AD·AC，
∴AB/AD=AC/AB。又∠BAD=∠CAB，
∴△ABD∽△ACB。
∴∠ABD=∠ACB，即∠ABE=∠ACF。
∵∠BAE=∠CAF，
∴△ABE∽△ACF。
(2)证明：
∵△ABE∽△ACF，
∴BE/CF=AB/AC。
∵BF=CF，
∴BE/BF=AB/AC。
∵△ABD∽△ACB，
∴BD/BC=AB/AC。
∵BC=2BF，
∴BD/(2BF)=AB/AC，
∴BD=2BE。
∴E为BD中点。
∵F为BC中点，
∴EF//AC。