第5页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
10. 已知二次函数$y= a(x-h)^2+k(a≠0)$,当$x= 1$时,$y= 1$;当$x= 8$时,$y= 8$,则下列说法中,正确的是 (
A.若$h= 4$,则$a<0$
B.若$h= 5$,则$a>0$
C.若$h= 6$,则$a<0$
D.若$h= 7$,则$a>0$
C
)A.若$h= 4$,则$a<0$
B.若$h= 5$,则$a>0$
C.若$h= 6$,则$a<0$
D.若$h= 7$,则$a>0$
答案:
10. C
11. 如图,抛物线$y= ax^2+c(a≠0)$经过正方形OABC的三个顶点A,B,C,其中点B在y轴上,则ac的值为 (
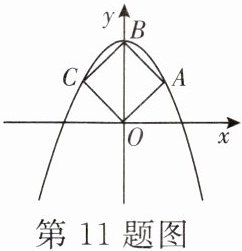
A.-1
B.-2
C.-3
D.-4
B
)
A.-1
B.-2
C.-3
D.-4
答案:
11. B
12. 如图,在平面直角坐标系xOy中,点B(2,-2),过点B分别作x轴、y轴的垂线,垂足各为A,C,二次函数$y= \frac{2}{3}(x-m)^2+k$的图象经过B,C两点.
(1)求该二次函数图象的顶点坐标.
(2)将该二次函数图象向上平移n个单位,使其顶点在四边形OABC内(含边界),求n的取值范围.
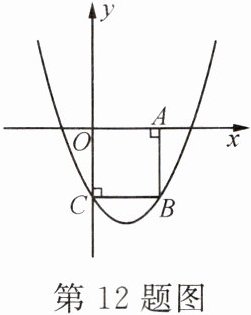
(1)求该二次函数图象的顶点坐标.
(2)将该二次函数图象向上平移n个单位,使其顶点在四边形OABC内(含边界),求n的取值范围.

答案:
12.
(1)$ (1,-\frac{8}{3}) $
(2)$ \frac{2}{3} \leqslant n \leqslant \frac{8}{3} $
(1)$ (1,-\frac{8}{3}) $
(2)$ \frac{2}{3} \leqslant n \leqslant \frac{8}{3} $
13. [创新意识]如图1,为了测量抛物线的开口大小,某数学兴趣小组将两把含有刻度的直尺垂直放置.
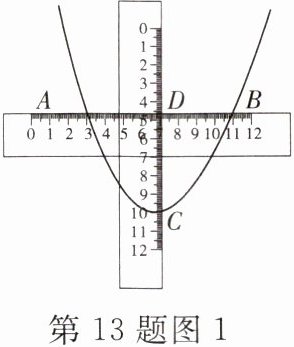
(1)如图2,在平面直角坐标系中,抛物线$y= a(x-h)^2+k(a≠0)$的顶点为C,该数学兴趣小组用水平和竖直直尺测量其水平跨度AB,竖直跨度CD,得到$AB= m$,$CD= n$,为了求出该抛物线的开口大小,该数学兴趣小组设计如下两种方案,请选择其中一种方案完善过程:
方案一:将二次函数$y= a(x-h)^2+k$平移,使得顶点C与原点O重合,此时抛物线表达式为$y= ax^2$.
①此时点B'的坐标为
②将点B'的坐标代入$y= ax^2$中,解得$a= $
方案二:设点C坐标为$(h,k)$.
①此时点B的坐标为
②将点B坐标代入$y= a(x-h)^2+k$中,解得$a= $
(2)如图3,已知平面直角坐标系xOy中有A,B两点,$AB= 4$,且$AB// x$轴,二次函数$C_1:y_1= 2(x+h)^2+k和C_2:y_2= a(x+h)^2+b$都经过A,B两点,且$C_1和C_2$的顶点P,Q距线段AB的距离之和为10,求a的值.
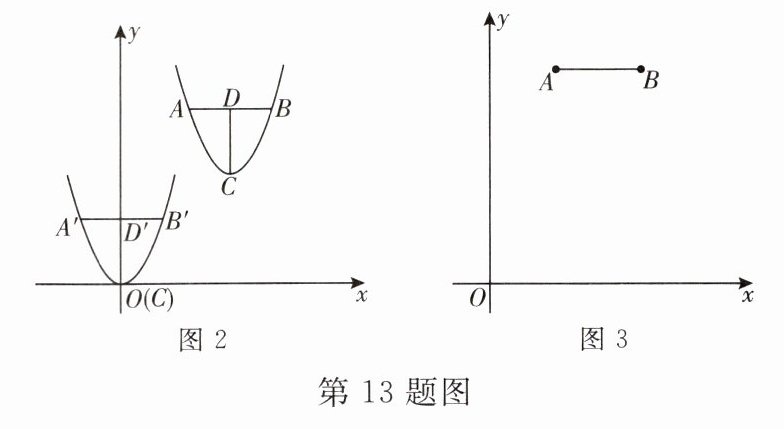

(1)如图2,在平面直角坐标系中,抛物线$y= a(x-h)^2+k(a≠0)$的顶点为C,该数学兴趣小组用水平和竖直直尺测量其水平跨度AB,竖直跨度CD,得到$AB= m$,$CD= n$,为了求出该抛物线的开口大小,该数学兴趣小组设计如下两种方案,请选择其中一种方案完善过程:
方案一:将二次函数$y= a(x-h)^2+k$平移,使得顶点C与原点O重合,此时抛物线表达式为$y= ax^2$.
①此时点B'的坐标为
$ (\frac{1}{2}m,n) $
.②将点B'的坐标代入$y= ax^2$中,解得$a= $
$ \frac{4n}{m^2} $
(用含m,n的式子表示).方案二:设点C坐标为$(h,k)$.
①此时点B的坐标为
$ (h+\frac{1}{2}m,k+n) $
.②将点B坐标代入$y= a(x-h)^2+k$中,解得$a= $
$ \frac{4n}{m^2} $
(用含m,n的式子表示).(选择一种方案即可) (2)如图3,已知平面直角坐标系xOy中有A,B两点,$AB= 4$,且$AB// x$轴,二次函数$C_1:y_1= 2(x+h)^2+k和C_2:y_2= a(x+h)^2+b$都经过A,B两点,且$C_1和C_2$的顶点P,Q距线段AB的距离之和为10,求a的值.

$ \pm \frac{1}{2} $
答案:
13.
(1)方案一:①$ (\frac{1}{2}m,n) $ ②$ \frac{4n}{m^2} $ 方案二:①$ (h+\frac{1}{2}m,k+n) $ ②$ \frac{4n}{m^2} $(选择一种方案即可)
(2)$ \pm \frac{1}{2} $
(1)方案一:①$ (\frac{1}{2}m,n) $ ②$ \frac{4n}{m^2} $ 方案二:①$ (h+\frac{1}{2}m,k+n) $ ②$ \frac{4n}{m^2} $(选择一种方案即可)
(2)$ \pm \frac{1}{2} $
查看更多完整答案,请扫码查看


