《2025年全效学习九年级数学上下册浙教版》

10. 如图,OA,OB,OC都是⊙O的半径,∠ACB= 2∠BAC.若AB= 4,BC= $\sqrt{5}$,则⊙O的半径为(C)

A.$\frac{3}{2}$
B.2
C.$\frac{5}{2}$
D.3

答案： C

11. 我国古代数学名著《九章算术》中有这样一道题：“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何？”其大意是：如图为一圆形木材,直径为25寸,要做成方形板材(四边形ABCD是矩形),使其厚度CD达到7寸,则宽BC为24寸.

答案： 24

12. 如图,在⊙O中,直径AB⊥CD于点E,连结CO并延长,交AD于点F.若CF⊥AD,则∠D的度数为60°.

答案： 60

13. 如图,在平面直角坐标系中,⊙P的圆心在x轴上,且经过点A(m,-3)和点B(-1,n),点C在第一象限的圆弧上,若∠ACB= 45°,则点P的坐标为(2,0).

答案： (2,0)

14. 如图,AB是半圆O的直径,C,D是半圆上的两点,且OD//AC,OD与BC相交于点E.
(1)求证：E是BC的中点.
(2)若BC= 8,DE= 3,求AB的长.

答案： 1. （1）证明：
因为$AB$是半圆$O$的直径，所以$\angle ACB = 90^{\circ}$（直径所对的圆周角是直角）。
又因为$OD// AC$，根据两直线平行，同位角相等，可得$\angle OEB=\angle ACB = 90^{\circ}$，即$OD\perp BC$。
由于$O$是$AB$的中点（半圆$O$中，$AB$为直径，圆心$O$为$AB$中点），在$\triangle ABC$中，$O$是$AB$中点，$OE\perp BC$，根据垂径定理的推论（垂直于弦的直径平分弦），所以$E$是$BC$的中点。
2. （2）解：
设$OB = OD = r$，因为$E$是$BC$中点，$BC = 8$，所以$BE=\frac{1}{2}BC = 4$。
已知$DE = 3$，则$OE=r - 3$。
在$Rt\triangle OBE$中，根据勾股定理$OB^{2}=OE^{2}+BE^{2}$，即$r^{2}=(r - 3)^{2}+4^{2}$。
展开$(r - 3)^{2}+4^{2}$得$r^{2}=r^{2}-6r + 9+16$。
移项可得：
$r^{2}-r^{2}+6r=9 + 16$。
$6r=25$，解得$r=\frac{25}{6}$。
所以$AB = 2r=\frac{25}{3}$。
综上，（1）得证；（2）$AB$的长为$\frac{25}{3}$。

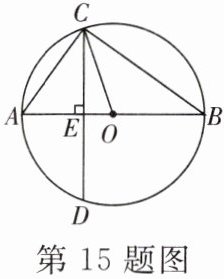
15. 如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连结AC,OC,BC.
(1)求证：∠BCO= ∠ACD.
(2)若AE= 4,BE= 16,求弦CD的长.

答案： 1. （1）证明：
因为$OB = OC$（圆的半径相等），根据等腰三角形的性质，所以$\angle BCO=\angle B$。
因为$AB$是$\odot O$的直径，$AB\perp CD$，根据垂径定理，$\overset{\frown}{BC}=\overset{\frown}{BD}$。
又因为同弧所对的圆周角相等，$\angle B$和$\angle ACD$都对$\overset{\frown}{BD}$，所以$\angle B = \angle ACD$。
综上，$\angle BCO=\angle ACD$。
2. （2）解：
已知$AE = 4$，$BE = 16$，则$AB=AE + BE=4 + 16 = 20$，所以$OA=OC=\frac{AB}{2}=10$，$OE=OA - AE=10 - 4 = 6$。
在$Rt\triangle OCE$中，根据勾股定理$a^{2}+b^{2}=c^{2}$（这里$c = OC$，$a = OE$，$b = CE$），可得$CE=\sqrt{OC^{2}-OE^{2}}$。
把$OC = 10$，$OE = 6$代入$CE=\sqrt{OC^{2}-OE^{2}}$，则$CE=\sqrt{10^{2}-6^{2}}=\sqrt{100 - 36}=\sqrt{64}=8$。
因为$AB\perp CD$，根据垂径定理，$CD = 2CE$。
所以$CD=2×8 = 16$。
综上，（1）证明如上；（2）弦$CD$的长为$16$。

16. [推理能力]如图,在平面直角坐标系中,点A(0,8),B是x轴负半轴上的动点,以OA为直径作圆,交AB于点D,连结OD.
(1)求证：∠AOD= ∠ABO.
(2)当∠ABO= 30°时,求点D到y轴的距离.
(3)$\frac{OD}{AB}$的最大值为______$\frac{1}{2}$.zyjl.cn/pic18/2025-08-18/c0d397e52a90478151d83ccf0bc68f18.jpg?x-oss-process=image/crop,x_1539,y_1617,w_300,h_264" data-title="">

答案： 1. （1）证明：
因为$OA$是圆的直径，所以$\angle ADO = 90^{\circ}$（直径所对的圆周角是直角）。
在$Rt\triangle ADO$和$Rt\triangle AOB$中，$\angle OAD=\angle BAO$（公共角）。
根据三角形内角和定理$\angle AOD + \angle OAD=90^{\circ}$，$\angle ABO+\angle OAD = 90^{\circ}$（直角三角形两锐角互余）。
所以$\angle AOD=\angle ABO$（同角的余角相等）。
2. （2）
过点$D$作$DE\perp y$轴于点$E$。
已知$A(0,8)$，则$OA = 8$。
在$Rt\triangle AOB$中，$\angle ABO = 30^{\circ}$，$\angle AOB = 90^{\circ}$，根据$\tan\angle ABO=\frac{OA}{OB}$，$\sin\angle ABO=\frac{OA}{AB}$。
因为$\sin30^{\circ}=\frac{OA}{AB}$，$OA = 8$，所以$AB=\frac{OA}{\sin30^{\circ}}=\frac{8}{\frac{1}{2}} = 16$，$OB=\sqrt{AB^{2}-OA^{2}}=\sqrt{16^{2}-8^{2}}=8\sqrt{3}$。
又因为$\angle AOD=\angle ABO = 30^{\circ}$，在$Rt\triangle ADO$中，$\cos\angle AOD=\frac{OE}{OD}$，$\sin\angle AOD=\frac{DE}{OD}$。
因为$\angle ADO = 90^{\circ}$，$\angle OAD = 60^{\circ}$，$\angle AOD = 30^{\circ}$，$OA = 8$，所以$OD=\frac{1}{2}OA = 4$（$30^{\circ}$角所对的直角边等于斜边的一半）。
则$DE = OD\sin\angle AOD$，$\angle AOD = 30^{\circ}$，$OD = 4$，所以$DE = 4×\frac{1}{2}=2$。
即点$D$到$y$轴的距离为$2$。
3. （3）
设$OB = x(x\gt0)$，则$AB=\sqrt{OA^{2}+OB^{2}}=\sqrt{64 + x^{2}}$。
因为$\angle AOD=\angle ABO$，$\angle ADO=\angle AOB = 90^{\circ}$，所以$\triangle ADO\sim\triangle AOB$（两角分别相等的两个三角形相似）。
则$\frac{OD}{OB}=\frac{OA}{AB}$，即$OD=\frac{OA\cdot OB}{AB}$。
所以$\frac{OD}{AB}=\frac{OA\cdot OB}{AB^{2}}=\frac{8x}{64 + x^{2}}$。
根据基本不等式$a + b\geqslant2\sqrt{ab}(a,b\gt0)$，当且仅当$a = b$时等号成立，对于$64 + x^{2}$，$64+x^{2}\geqslant2\sqrt{64x^{2}} = 16|x|$（因为$x\gt0$，所以$64 + x^{2}\geqslant16x$）。
则$\frac{8x}{64 + x^{2}}\leqslant\frac{8x}{16x}=\frac{1}{2}$，当且仅当$x = 8$时取等号。
故答案依次为：（1）证明见上述过程；（2）$2$；（3）$\frac{1}{2}$。