1. 下列说法中,正确的是 (
A.正有理数和负有理数统称有理数
B.整数和分数统称有理数
C.正整数和负整数统称整数
D.1,0,$-\frac{1}{2}和\pi$都是有理数
B
)A.正有理数和负有理数统称有理数
B.整数和分数统称有理数
C.正整数和负整数统称整数
D.1,0,$-\frac{1}{2}和\pi$都是有理数
答案:
B
2. 把下列各数填入相应的横线上:
$-3.5$,$-\frac{1}{2}$,$3.2$,$8.1$,0,$1.3$,$-20\%$,5,$\frac{1}{4}$,$-7$。
整数:
分数:
负分数:
自然数:
非负数:
非正数:
$-3.5$,$-\frac{1}{2}$,$3.2$,$8.1$,0,$1.3$,$-20\%$,5,$\frac{1}{4}$,$-7$。
整数:
0,5,-7
;分数:
-3.5,-$\frac{1}{2}$,3.2,8.1,1.3,-20%,$\frac{1}{4}$
;负分数:
-3.5,-$\frac{1}{2}$,-20%
;自然数:
0,5
;非负数:
3.2,8.1,0,1.3,5,$\frac{1}{4}$
;非正数:
-3.5,-$\frac{1}{2}$,0,-20%,-7
。
答案:
0,5,-7;-3.5,-$\frac{1}{2}$,3.2,8.1,1.3,-20%,$\frac{1}{4}$;-3.5,-$\frac{1}{2}$,-20%;0,5;3.2,8.1,0,1.3,5,$\frac{1}{4}$;-3.5,-$\frac{1}{2}$,0,-20%,-7
3. 在$+5$,$-4$,$+\vert-3.14\vert$,$-(+\frac{3}{2})$,$20\%$,$-\vert-\frac{3}{4}\vert$中,正数是
+5,+|-3.14|,20%
。
答案:
+5,+|-3.14|,20%
4.(1)如果把商店盈利100元记为$+100$元,那么亏损20元记为
(2)如果把仪表的指针逆时针转3圈记为$+3$圈,那么$-2$圈表示仪表的指针
(3)如果正常水位为0米,水位高于正常水位0.2米时记为$+0.2$米,那么$-0.5$米表示
-20
元。(2)如果把仪表的指针逆时针转3圈记为$+3$圈,那么$-2$圈表示仪表的指针
顺时针转2圈
。(3)如果正常水位为0米,水位高于正常水位0.2米时记为$+0.2$米,那么$-0.5$米表示
水位低于正常水位0.5米
。
答案:
(1)-20
(2)顺时针转2圈
(3)水位低于正常水位0.5米
(1)-20
(2)顺时针转2圈
(3)水位低于正常水位0.5米
5. 某项科学研究以45分钟为一个时间单位,并把每天上午10时记为0,10时以前记为负,10时以后记为正。例如:上午9:15记为$-1$,上午10:45记为1。依此类推,上午7:45应记为
-3
,中午12:15应记为3
。
答案:
-3 3
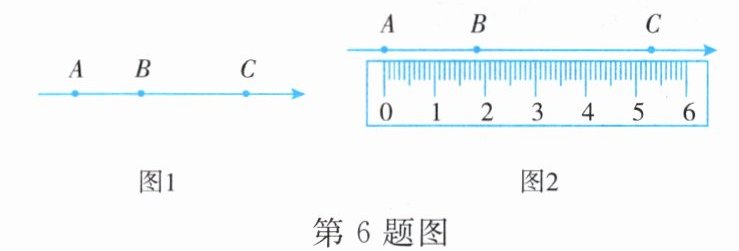
6. 如图1,A,B,C是数轴上从左到右排列的三个点,分别对应的数为$-2$,b,4。某同学将刻度尺如图2放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度1.8cm,点C对应刻度5.4cm。则数轴上点B所对应的数b为 (
A.2
B.1
C.0
D.$-1$
C
)
A.2
B.1
C.0
D.$-1$
答案:
C
7. 绝对值不大于$5\frac{1}{3}$的所有正整数的积等于
120
。
答案:
120
8. 如图,图中数轴的单位长度为1。请回答下列问题:
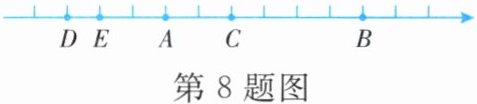
(1)如果点A,B表示的数互为相反数,那么点C表示的数是多少?
(2)如果点D,B表示的数互为相反数,那么点C表示的数是正数还是负数?图中表示的5个点中,哪一个点表示的数的绝对值最小?最小的绝对值是多少?

(1)如果点A,B表示的数互为相反数,那么点C表示的数是多少?
(2)如果点D,B表示的数互为相反数,那么点C表示的数是正数还是负数?图中表示的5个点中,哪一个点表示的数的绝对值最小?最小的绝对值是多少?
答案:
(1)-1
(2)点C表示的数是正数,点C表示的数的绝对值最小,最小的绝对值是0.5
(1)-1
(2)点C表示的数是正数,点C表示的数的绝对值最小,最小的绝对值是0.5
9. 如图,A,B分别为数轴上的两点,点A对应的数为$-20$,点B对应的数为100。

(1)请写出与A,B两点距离相等的点M所对应的数。
(2)现有一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度向右运动。设两只电子蚂蚁在数轴上的点C相遇,你知道点C对应的数是多少吗?
(3)若当电子蚂蚁P从点B出发时,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度也向左运动。当它们运动多少时间时,两只蚂蚁间的距离为20个单位长度?

(1)请写出与A,B两点距离相等的点M所对应的数。
(2)现有一只电子蚂蚁P从点B出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度向右运动。设两只电子蚂蚁在数轴上的点C相遇,你知道点C对应的数是多少吗?
(3)若当电子蚂蚁P从点B出发时,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从点A出发,以4个单位长度/秒的速度也向左运动。当它们运动多少时间时,两只蚂蚁间的距离为20个单位长度?
答案:
1. (1)
设点$M$对应的数为$x$。
根据数轴上两点间距离公式$\vert a - b\vert$,$A$对应的数为$-20$,$B$对应的数为$100$,因为$\vert x-(-20)\vert=\vert x - 100\vert$,即$x + 20=100 - x$($x+20$与$100 - x$同号)。
移项可得$x+x=100 - 20$,$2x = 80$,解得$x = 40$。
2. (2)
解:设$t$秒后两只蚂蚁相遇。
点$A$对应的数为$-20$,点$B$对应的数为$100$,则$AB$的距离为$\vert100-(-20)\vert=120$个单位长度。
电子蚂蚁$P$的速度$v_{P}=6$个单位长度/秒,电子蚂蚁$Q$的速度$v_{Q}=4$个单位长度/秒,根据$s = v_{P}t+v_{Q}t$($s$为$AB$间距离),可得$120=(6 + 4)t$。
即$10t = 120$,解得$t = 12$秒。
那么点$Q$运动的距离为$s_{Q}=4t$,把$t = 12$代入,$s_{Q}=4×12 = 48$。
因为点$Q$从$A(-20)$出发向右运动,所以点$C$对应的数为$-20 + 48=28$。
3. (3)
解:设运动$t$秒时,两只蚂蚁间的距离为$20$个单位长度。
电子蚂蚁$P$从$B(100)$出发向左运动,$t$秒后$P$对应的数为$100-6t$;电子蚂蚁$Q$从$A(-20)$出发向左运动,$t$秒后$Q$对应的数为$-20-4t$。
①当$P$在$Q$右侧$20$个单位长度时,$(100-6t)-(-20 - 4t)=20$。
去括号得$100-6t + 20+4t = 20$。
移项得$-6t+4t=20-(100 + 20)$。
合并同类项得$-2t=20 - 120$,$-2t=-100$,解得$t = 50$。
②当$Q$在$P$右侧$20$个单位长度时,$(-20-4t)-(100 - 6t)=20$。
去括号得$-20-4t-100 + 6t = 20$。
移项得$-4t+6t=20+(20 + 100)$。
合并同类项得$2t=140$,解得$t = 70$。
综上,(1)点$M$对应的数为$40$;(2)点$C$对应的数为$28$;(3)运动$50$秒或$70$秒时,两只蚂蚁间的距离为$20$个单位长度。
设点$M$对应的数为$x$。
根据数轴上两点间距离公式$\vert a - b\vert$,$A$对应的数为$-20$,$B$对应的数为$100$,因为$\vert x-(-20)\vert=\vert x - 100\vert$,即$x + 20=100 - x$($x+20$与$100 - x$同号)。
移项可得$x+x=100 - 20$,$2x = 80$,解得$x = 40$。
2. (2)
解:设$t$秒后两只蚂蚁相遇。
点$A$对应的数为$-20$,点$B$对应的数为$100$,则$AB$的距离为$\vert100-(-20)\vert=120$个单位长度。
电子蚂蚁$P$的速度$v_{P}=6$个单位长度/秒,电子蚂蚁$Q$的速度$v_{Q}=4$个单位长度/秒,根据$s = v_{P}t+v_{Q}t$($s$为$AB$间距离),可得$120=(6 + 4)t$。
即$10t = 120$,解得$t = 12$秒。
那么点$Q$运动的距离为$s_{Q}=4t$,把$t = 12$代入,$s_{Q}=4×12 = 48$。
因为点$Q$从$A(-20)$出发向右运动,所以点$C$对应的数为$-20 + 48=28$。
3. (3)
解:设运动$t$秒时,两只蚂蚁间的距离为$20$个单位长度。
电子蚂蚁$P$从$B(100)$出发向左运动,$t$秒后$P$对应的数为$100-6t$;电子蚂蚁$Q$从$A(-20)$出发向左运动,$t$秒后$Q$对应的数为$-20-4t$。
①当$P$在$Q$右侧$20$个单位长度时,$(100-6t)-(-20 - 4t)=20$。
去括号得$100-6t + 20+4t = 20$。
移项得$-6t+4t=20-(100 + 20)$。
合并同类项得$-2t=20 - 120$,$-2t=-100$,解得$t = 50$。
②当$Q$在$P$右侧$20$个单位长度时,$(-20-4t)-(100 - 6t)=20$。
去括号得$-20-4t-100 + 6t = 20$。
移项得$-4t+6t=20+(20 + 100)$。
合并同类项得$2t=140$,解得$t = 70$。
综上,(1)点$M$对应的数为$40$;(2)点$C$对应的数为$28$;(3)运动$50$秒或$70$秒时,两只蚂蚁间的距离为$20$个单位长度。
查看更多完整答案,请扫码查看


