《2025年全效学习七年级数学上册浙教版》

1. 下列变形中,运用加法运算律正确的是(B)
A.3+(-5)= 5+3
B.4+(-6)+3= (-6)+4+3
C.[5+(-2)]+4= [5+(-4)]+2
D.$\frac{1}{6}+(-1)+(+\frac{5}{6})= (\frac{1}{6}+\frac{5}{6})+(+1)$

答案： B

2. $\frac{2}{3}+(-2.5)+3.5+(-\frac{2}{3})= [\frac{2}{3}+(-\frac{2}{3})]+[(-2.5)+3.5]$,这个计算运用了 (C)
A.加法交换律
B.加法结合律
C.加法交换律和加法结合律
D.以上均不对

答案： C

3. 运用加法运算律计算$(+6\frac{1}{3})+(-18)+(+4\frac{2}{3})+(-6.8)+18+(-3.2)$,最简便的是 (D)
A.$[(+6\frac{1}{3})+(+4\frac{2}{3})+18]+[(-18)+(-6.8)+(-3.2)]$
B.$[(+6\frac{1}{3})+(-6.8)+(+4\frac{2}{3})]+[(-18)+18+(-3.2)]$
C.$[(+6\frac{1}{3})+(-18)]+[(+4\frac{2}{3})+(-6.8)]+[18+(-3.2)]$
D.$[(+6\frac{1}{3})+(+4\frac{2}{3})]+[(-18)+18]+[(-3.2)+(-6.8)]$

答案： D

4. 计算：(1)$6+(-4)+(-6)= $-4；
(2)$(-1\frac{3}{5})+2\frac{1}{7}+(-2\frac{2}{5})+(-3\frac{1}{7})= $-5。

答案：
(1)-4
(2)-5

5. 计算：
(1)$23+(-17)+6+(-22)$；
(2)$1+(-\frac{1}{2})+\frac{1}{3}+(-\frac{1}{6})$；
(3)$(-2.71)+(+4.96)+(-7.29)+(-4.96)$；
(4)$(-2.125)+(+3\frac{1}{5})+(+5\frac{1}{8})+(-3.2)$。

答案：
(1)-10
(2)$\frac{2}{3}$
(3)-10
(4)3

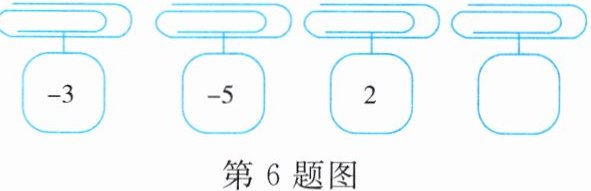
6. 如图,每个曲别针下方挂着一张写有整数的卡片,从左到右,第1个至第3个曲别针所挂卡片上的整数分别为-3,-5,2。
(1)求前三个曲别针所挂卡片上数的和。
(2)若后两个数绝对值的和比前两个数的和的绝对值大3,请求出第4个数。

答案：
(1)-6
(2)$\pm 9$