《2025年点拨训练八年级数学上册沪科版安徽专版》

10. 一次函数$y = - 2 x + 8的图象与正比例函数y = k x的图象相交于点A ( 2, b )$,点$M$,$N分别在一次函数y = - 2 x + 8和正比例函数y = k x$的图象上,且$MN // x$轴. 则
(1)$k = $2；
(2)当$MN = 2$时,点$M$的坐标是$(1,6)$或$(3,2)$.

答案：
(1)2
(2)$(1,6)$或$(3,2)$

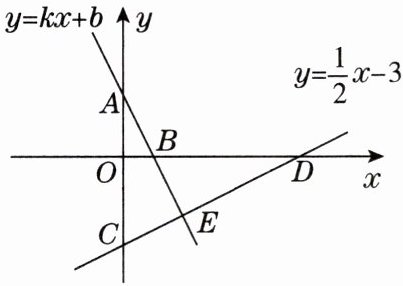
11. (20分)如图,直线$AB$：$y = k x + b与坐标轴的交点分别为A ( 0,2 )$,$B ( 1,0 )$,直线$CD$：$y = \dfrac { 1 } { 2 } x - 3与坐标轴交于C$,$D$两点.
(1)求直线$AB与直线CD的交点E$的坐标；
(2)直接写出不等式$k x + b \geqslant \dfrac { 1 } { 2 } x - 3$的解集；
(3)求四边形$OBEC$的面积.

答案： 解：
(1)点 E 的坐标是$(2,-2)$.
(2)$x\leqslant 2$.
(3)四边形 OBEC 的面积为 4.

12. (20分)学校通过劳动教育促进学生德智体美全面发展,计划组织八年级学生到“开心”农场开展劳动实践活动. 到达农场后分组进行劳动,若每名老师带38名学生,则还剩6名学生没老师带；若每名老师带40名学生,则有1名老师少带6名学生. 劳动实践活动结束后,学校租车送师生返校,租车总费用限额2300元,现有甲、乙两种大型客车,它们的载客量和租金如表所示：

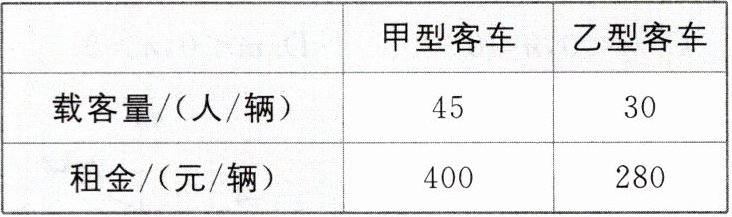
(1)参加本次劳动实践活动的老师和学生各有多少名？
(2)租车返校时,既要保证所有师生都有座位,又要保证每辆车上至少有1名老师,则共需租车______辆；
(3)学校有哪几种租车方案？最少租车总费用是多少？
解：(1)参加本次劳动实践活动的老师有 6 名,学生有234 名.
6
(3)设租甲型客车 m 辆,则租乙型客车$(6-m)$辆,设租车总费用为 n 元,由题意得$n=400m+280×(6-m),$整理得$n=120m+1680$,因为租车总费用限额 2300元,所以$120m+1680\leqslant 2300$,所以$m\leqslant \frac {31}{6}$.因为要保证240 名师生都有座位,所以$45m+30×(6-m)\geqslant 240,$所以$m\geqslant 4$.又因为 m 为整数,所以$m=4$或 5.所以学校有两种租车方案：方案一:租 4 辆甲型客车,2 辆乙型客车；方案二:租 5 辆甲型客车,1 辆乙型客车.因为$120＞0$,所以 n 随 m 的增大而增大,所以当$m=4$时,n 最小,此时$n=120×4+1680=2160.$即最少租车总费用为 2160 元.

答案： 解：
(1)参加本次劳动实践活动的老师有 6 名,学生有234 名.
(2)6
(3)设租甲型客车 m 辆,则租乙型客车$(6-m)$辆,设租车总费用为 n 元,由题意得$n=400m+280×(6-m),$整理得$n=120m+1680$,因为租车总费用限额 2300元,所以$120m+1680\leqslant 2300$,所以$m\leqslant \frac {31}{6}$.因为要保证240 名师生都有座位,所以$45m+30×(6-m)\geqslant 240,$所以$m\geqslant 4$.又因为 m 为整数,所以$m=4$或 5.所以学校有两种租车方案：方案一:租 4 辆甲型客车,2 辆乙型客车；方案二:租 5 辆甲型客车,1 辆乙型客车.因为$120＞0$,所以 n 随 m 的增大而增大,所以当$m=4$时,n 最小,此时$n=120×4+1680=2160.$即最少租车总费用为 2160 元.