11. 如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 7\mathrm{cm}$,$BC = 3\mathrm{cm}$,$CD为AB$边上的高。点$E从点B$出发,在直线$BC上以2\mathrm{cm/s}$的速度移动,过点$E作BC的垂线交直线CD于点F$。
(1) 若$\angle ECF= \alpha$,则$\angle CAB= $
(2) 当点$E$运动
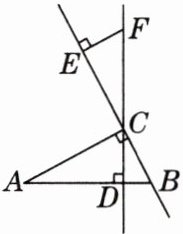
(1) 若$\angle ECF= \alpha$,则$\angle CAB= $
α
(用含$\alpha$的代数式表示);(2) 当点$E$运动
2 或 5
s 时,$CF = AB$。
答案:
(1)α
(2)2 或 5
(1)α
(2)2 或 5
12.(14 分)如图,工人师傅要检查人字梁的$\angle B和\angle C$是否相等,但他身边没有量角器,只有一个刻度尺。他是这样操作的:
①分别在$BA和CA上取BE = CG$;
②在$BC上取BD = CF$;
③连接$DE$,$FG$,若量出$DE的长等于FG$的长,则说明$\angle B和\angle C$是相等的,他的这种做法合理吗?为什么?
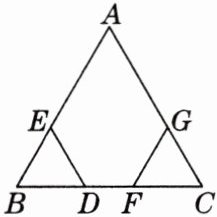
①分别在$BA和CA上取BE = CG$;
②在$BC上取BD = CF$;
③连接$DE$,$FG$,若量出$DE的长等于FG$的长,则说明$\angle B和\angle C$是相等的,他的这种做法合理吗?为什么?

答案:
解:这种做法合理.
理由:在△BDE 和△CFG 中,
∵BE=CG,BD=CF,DE=FG.
∴△BDE≌△CFG(SSS).
∴∠B=∠C.
理由:在△BDE 和△CFG 中,
∵BE=CG,BD=CF,DE=FG.
∴△BDE≌△CFG(SSS).
∴∠B=∠C.
13.(15 分)如图,$DE\perp AB交AB的延长线于点E$,$DF\perp AC于点F$,$BD = CD$,$BE = CF$。
(1) 求证:$DE = DF$;
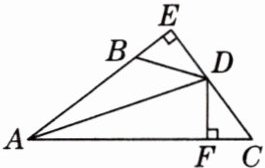
(2) 已知$AC = 20$,$BE = 4$,求$AB$的长。
(1) 求证:$DE = DF$;

(2) 已知$AC = 20$,$BE = 4$,求$AB$的长。
答案:
(1)证明:
∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在 Rt△BED 和 Rt△CFD 中,$\left\{\begin{array}{l} BD=CD,\\ BE=CF,\end{array}\right. $
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF.
(2)解:AB=12.
(1)证明:
∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°.
在 Rt△BED 和 Rt△CFD 中,$\left\{\begin{array}{l} BD=CD,\\ BE=CF,\end{array}\right. $
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF.
(2)解:AB=12.
14.(16 分)如图,在$\triangle ABC和\triangle AED$中,$AB = AC$,$AE = AD$,$\angle BAC= \angle EAD$,且点$E$,$A$,$B$在同一直线上,点$C$,$D在EB$的同侧,连接$BD$,$CE交于点M$。
(1) 求证:$\triangle ABD\cong\triangle ACE$;
(2) 若$\angle CAD = 110^{\circ}$,求$\angle DME$的度数。
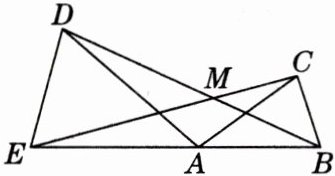
(1) 求证:$\triangle ABD\cong\triangle ACE$;
(2) 若$\angle CAD = 110^{\circ}$,求$\angle DME$的度数。

答案:
(1)证明:
∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,
即∠DAB=∠EAC.
在△ABD 和△ACE 中,$\left\{\begin{array}{l} AD=AE,\\ ∠DAB=∠EAC,\\ AB=AC,\end{array}\right. $
∴△ABD≌△ACE(SAS).
(2)解:∠DME=35°.
(1)证明:
∵∠BAC=∠EAD,
∴∠BAC+∠DAC=∠EAD+∠DAC,
即∠DAB=∠EAC.
在△ABD 和△ACE 中,$\left\{\begin{array}{l} AD=AE,\\ ∠DAB=∠EAC,\\ AB=AC,\end{array}\right. $
∴△ABD≌△ACE(SAS).
(2)解:∠DME=35°.
查看更多完整答案,请扫码查看


