13. 如图,D,E分别是△ABC的AC,AB边上的点,将△ABC沿DE折叠使点A落在点A'处.
(1)若∠1= 100°,∠2= 50°,则∠A的度数为
(2)若D,E始终在AC,AB边上时(不和点A重合),∠1= m,∠2= n,且∠A为锐角,当点A'落在∠BAC内部时,则∠A的度数为
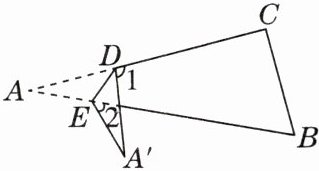
(1)若∠1= 100°,∠2= 50°,则∠A的度数为
25°
;(2)若D,E始终在AC,AB边上时(不和点A重合),∠1= m,∠2= n,且∠A为锐角,当点A'落在∠BAC内部时,则∠A的度数为
$\frac{1}{2}(m+n)$
.(用含m,n的代数式表示)
答案:
(1)25°;
(2)$\frac{1}{2}(m+n)$
(1)25°;
(2)$\frac{1}{2}(m+n)$
14. (14分)梦雪的爸爸将一段长为30m的渔网围成一个三角形,已知第一条边长为a m,第二条边长比第一条边长的2倍还多2m.
(1)请用a表示第三条边长;
(2)请求出a的取值范围.
(1)请用a表示第三条边长;
(2)请求出a的取值范围.
答案:
(1)
∵第一条边长为a m,
∴第二条边长为(2a+2)m,又
∵总长为30 m,
∴第三条边长为30-a-(2a+2)=28-3a(m).
(2)$\frac{13}{3}<a<\frac{13}{2}$.
(1)
∵第一条边长为a m,
∴第二条边长为(2a+2)m,又
∵总长为30 m,
∴第三条边长为30-a-(2a+2)=28-3a(m).
(2)$\frac{13}{3}<a<\frac{13}{2}$.
15. (16分)如图,D,E,F分别是△ABC的边AB,AC,BC上的点,有如下三个论断:①DE//BC;②DF//AC;③∠1= ∠C.
(1)请从这三个论断中选择两个作为条件,余下的一个作为结论,构成一个真命题. 试用“如果……那么……”的形式写出来(写出所有的真命题,不需要说明理由);
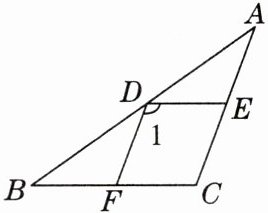
(2)请你在上述真命题中选择一个进行证明并说明推理依据.
(1)请从这三个论断中选择两个作为条件,余下的一个作为结论,构成一个真命题. 试用“如果……那么……”的形式写出来(写出所有的真命题,不需要说明理由);

(2)请你在上述真命题中选择一个进行证明并说明推理依据.
答案:
(1)如果①②,那么③;如果①③,那么②;如果②③,那么①.
(2)(答案不唯一)已知:DE//BC,∠1=∠C. 求证:DF//AC. 证明:
∵DE//BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∵∠1=∠C(已知),
∴∠AED=∠1(等量代换),
∴DF//AC(内错角相等,两直线平行).
(1)如果①②,那么③;如果①③,那么②;如果②③,那么①.
(2)(答案不唯一)已知:DE//BC,∠1=∠C. 求证:DF//AC. 证明:
∵DE//BC(已知),
∴∠AED=∠C(两直线平行,同位角相等).
∵∠1=∠C(已知),
∴∠AED=∠1(等量代换),
∴DF//AC(内错角相等,两直线平行).
16. (18分)在∠MAN中,点B,C分别是AM,AN上一点,∠ABC和∠ACB的平分线交于点P.
(1)如图①,若∠MAN= 90°,求∠P的度数;
(2)如图②,若∠A= $\frac{1}{2}$∠P,求∠A的度数;
(3)如图③,∠CBM和∠BCN的平分线交于点Q,直接写出∠P和∠Q之间的数量关系,不需要证明.
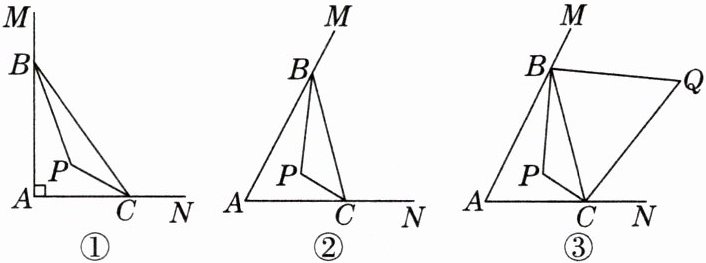
(1)如图①,若∠MAN= 90°,求∠P的度数;
(2)如图②,若∠A= $\frac{1}{2}$∠P,求∠A的度数;
(3)如图③,∠CBM和∠BCN的平分线交于点Q,直接写出∠P和∠Q之间的数量关系,不需要证明.

答案:
(1)∠P=135°.
(2)∠A=60°.
(3)∠P+∠Q=180°.
(1)∠P=135°.
(2)∠A=60°.
(3)∠P+∠Q=180°.
查看更多完整答案,请扫码查看


