1. 下列四个图形中,是全等形的是(
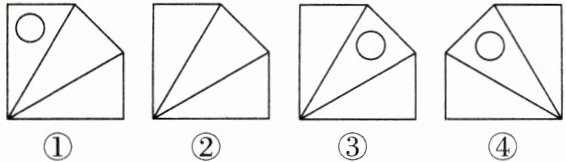
A.①和②
B.③和④
C.①和③
D.②和③
B
)
A.①和②
B.③和④
C.①和③
D.②和③
答案:
B
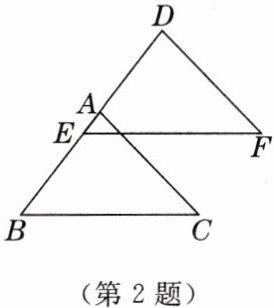
2. 如图,$\triangle ABC\cong\triangle DEF$,$AD = 8$,$AE = 2$,则$AB$的长是(
A.10
B.8
C.6
D.4
A
)
A.10
B.8
C.6
D.4
答案:
A
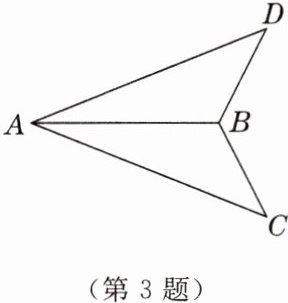
3. 如图,在$\triangle ABD和\triangle ABC$中,$\angle DAB= \angle CAB$,添加下列条件不能判定$\triangle ABD\cong\triangle ABC$的是(
A.$BD = BC$
B.$\angle D= \angle C$
C.$\angle ABD= \angle ABC$
D.$AD = AC$
A
)
A.$BD = BC$
B.$\angle D= \angle C$
C.$\angle ABD= \angle ABC$
D.$AD = AC$
答案:
A
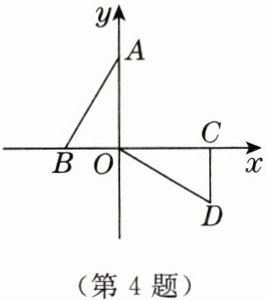
4. 如图,在平面直角坐标系中,已知$A(0,5)$,$B(-3,0)$。若$\triangle AOB\cong\triangle OCD$,则点$D$的坐标是(
A.$(5,-3)$
B.$(-3,5)$
C.$(3,5)$
D.$(3,-5)$
A
)
A.$(5,-3)$
B.$(-3,5)$
C.$(3,5)$
D.$(3,-5)$
答案:
A
5. 如图,网格中有$\triangle ABC及线段DE$,在网格中找一点$F$(必在格点上),使$\triangle DEF与\triangle ABC$全等,这样的点$F$有(
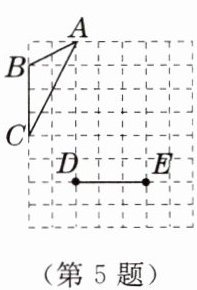
A.1 个
B.2 个
C.3 个
D.4 个
D
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:
D
6. 如图,在四边形$OAPE$中,点$D$,$B分别在边OA$,$OE$上,$\triangle APD\cong\triangle BPE$,下列结论不一定正确的是(
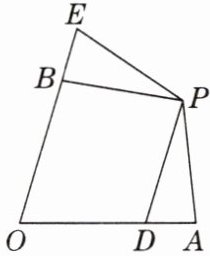
A.$PB = PA$
B.$OB = PD$
C.$\angle BPA= \angle DPE$
D.$\angle OBP+\angle A = 180^{\circ}$
B
)
A.$PB = PA$
B.$OB = PD$
C.$\angle BPA= \angle DPE$
D.$\angle OBP+\angle A = 180^{\circ}$
答案:
B
7. 如图,$AE\perp AB$,且$AE = AB$,$BC\perp CD$,且$BC = CD$,按照图中所标注的数据计算图中实线所围成的图形的面积为(
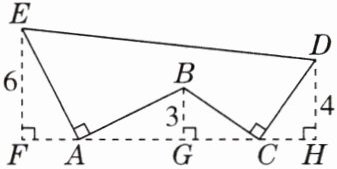
A.30
B.50
C.60
D.80
B
)
A.30
B.50
C.60
D.80
答案:
B
8. 如图,用纸板挡住三角形的一部分后,仍能画出与此三角形全等的三角形,其全等的依据是
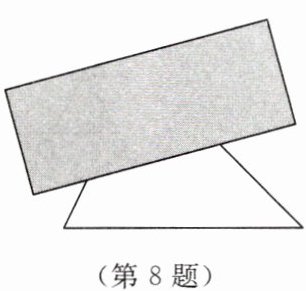
ASA
。
答案:
ASA
9. 如图,在边长为 1 的小正方形组成的网格中,给出以下结论:①$AB = CD$;②$AB\perp CD$;③$\angle 1与\angle 2$互补,其中正确的是
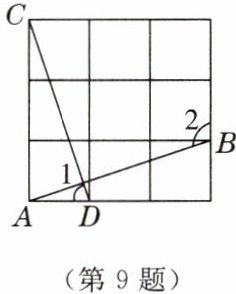
①②③
(填序号)。
答案:
①②③
10. 如图,$BE\perp AE$,$CF\perp BE$,垂足分别为$E$,$F$,$D是线段EF$的中点,$CF = BF$,若$AE = 4$,$DE = 3$,则$\triangle ABC$的面积是
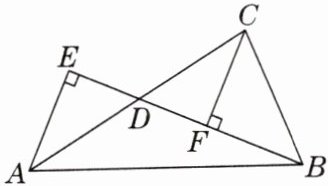
28
。
答案:
28
查看更多完整答案,请扫码查看


