1. 一次函数$y = ax + b和y = cx + d$的图象如图所示,关于$x$,$y的方程组\begin{cases}y = ax + b, \\ y = cx + d\end{cases} 的解为\begin{cases}x = m, \\ y = n,\end{cases} $则下列结论正确的是(
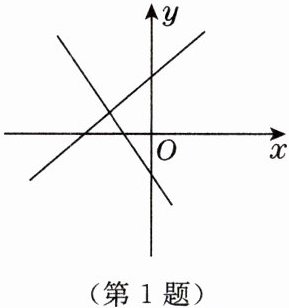
A.$m > 0$,$n > 0$
B.$m > 0$,$n < 0$
C.$m < 0$,$n < 0$
D.$m < 0$,$n > 0$
D
)
A.$m > 0$,$n > 0$
B.$m > 0$,$n < 0$
C.$m < 0$,$n < 0$
D.$m < 0$,$n > 0$
答案:
D
2. 如图,函数$y = ax + b和y = kx的图象交于点P$,根据图象,可得关于$x$,$y的二元一次方程组\begin{cases}ax - y + b = 0, \\ kx - y = 0\end{cases} $的解是(
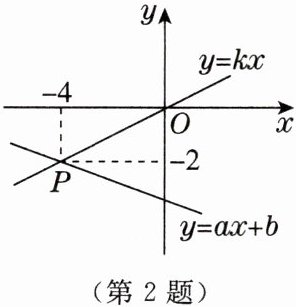
A.$\begin{cases}x = - 4, \\ y = - 2\end{cases} $
B.$\begin{cases}x = 4, \\ y = 2\end{cases} $
C.$\begin{cases}x = - 2, \\ y = - 4\end{cases} $
D.$\begin{cases}x = 2, \\ y = 4\end{cases} $
A
)
A.$\begin{cases}x = - 4, \\ y = - 2\end{cases} $
B.$\begin{cases}x = 4, \\ y = 2\end{cases} $
C.$\begin{cases}x = - 2, \\ y = - 4\end{cases} $
D.$\begin{cases}x = 2, \\ y = 4\end{cases} $
答案:
A
3. 若一次函数$y - k _ { 1 } x = b _ { 1 }与y - k _ { 2 } x = b _ { 2 }$的图象没有交点,则关于$x$,$y的方程组\begin{cases}y - k _ { 1 } x = b _ { 1 }, \\ y - k _ { 2 } x = b _ { 2 }\end{cases} $的解的情况是(
A.有无数组解
B.有两组解
C.只有一组解
D.没有解
D
)A.有无数组解
B.有两组解
C.只有一组解
D.没有解
答案:
D
4. 直线$y = - 3 x - 2与y = x + 6$的交点坐标是(
A.$( 1,7 )$
B.$( - 3,3 )$
C.$( - 2,4 )$
D.$( 2,8 )$
C
)A.$( 1,7 )$
B.$( - 3,3 )$
C.$( - 2,4 )$
D.$( 2,8 )$
答案:
C
5. 把方程$x + y = 2的两组解\begin{cases}x = 1, \\ y = 1\end{cases} 和\begin{cases}x = 0, \\ y = 2\end{cases} 组成有序数对( 1,1 )$,$( 0,2 )$,过这两点画直线$l$,下列各点不在直线$l$上的是(
A.$( 4, - 2 )$
B.$( 2,1 )$
C.$( - 2,4 )$
D.$( - 4,6 )$
B
)A.$( 4, - 2 )$
B.$( 2,1 )$
C.$( - 2,4 )$
D.$( - 4,6 )$
答案:
B
6. 如图,函数$y _ { 1 } = - 2 x与y _ { 2 } = a x + 3的图象相交于点A ( m, 2 )$,则关于$x的不等式组- 2 x > a x + 3 > 0$的解集是(
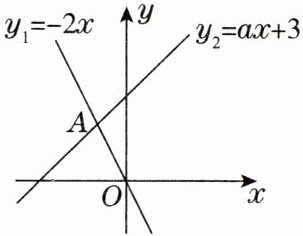
A.$x > - 1$
B.$- 1 < x < 0$
C.$x < - 1$
D.$- 3 < x < - 1$
D
)
A.$x > - 1$
B.$- 1 < x < 0$
C.$x < - 1$
D.$- 3 < x < - 1$
答案:
D
7. 随着暑假临近,某游泳馆推出了甲、乙两种消费卡,设消费次数为$x$时,所需费用为$y$元,且$y与x$的函数关系如图所示. 根据图中信息判断,下列说法错误的是(
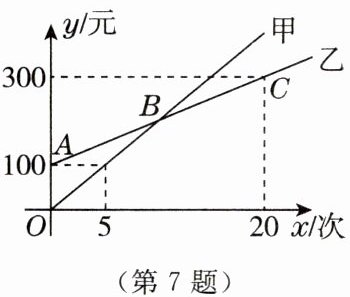
A.甲种消费卡为20元/次
B.$y _ { \text {乙 } } = 10 x + 100$
C.点$B的坐标为( 10,200 )$
D.洋洋爸爸准备了240元钱用于洋洋在该游泳馆消费,选择甲种消费卡划算
D
)
A.甲种消费卡为20元/次
B.$y _ { \text {乙 } } = 10 x + 100$
C.点$B的坐标为( 10,200 )$
D.洋洋爸爸准备了240元钱用于洋洋在该游泳馆消费,选择甲种消费卡划算
答案:
D
8. 如图,直线$y = - x + 3与y = m x + n$交点的横坐标为1,则关于$x$,$y的二元一次方程组\begin{cases}x + y = 3, \\ - m x + y = n\end{cases} $的解为
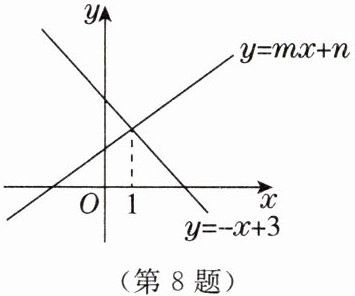
$\left\{\begin{array}{l} x=1,\\ y=2\end{array}\right. $
.
答案:
$\left\{\begin{array}{l} x=1,\\ y=2\end{array}\right. $
9. 在平面直角坐标系中,若直线$y = - 2 x - 4与y = 4 x + b$的交点在第三象限,则$b$的取值范围是
$-4<b<8$
.
答案:
$-4<b<8$
查看更多完整答案,请扫码查看


