《2025年点拨训练八年级数学上册沪科版安徽专版》

12. (12 分)已知关于 $ x $ 的一次函数 $ y = (4 + 2m)x + m - 4 $。
(1)当 $ y $ 随 $ x $ 的增大而减小时,求 $ m $ 的取值范围；
(2)当该函数图象与 $ y $ 轴的交点在 $ x $ 轴下方时,求 $ m $ 的取值范围；
(3)当该函数图象经过第一、三、四象限时,求 $ m $ 的取值范围。

答案： 解：
(1)m＜-2.
(2)m＜4且m≠-2.
(3)-2＜m＜4.

13. (14 分)在如图所示的平面直角坐标系中画出函数 $ y = 2x + 6 $ 的图象,结合图象：
(1)求方程 $ 2x + 6 = 0 $ 的解；
(2)求不等式 $ 2x + 6 ＜ 0 $ 的解集；
(3)若 $ -2 \leq y \leq 3 $,直接写出 $ x $ 的取值范围。

答案：
解：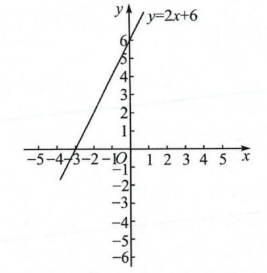
(1)x=-3.
(2)x＜-3.
(3)当-2≤y≤3时，-4≤x≤-3/2.

14. (16 分)阶梯电价的收费方式如下：第一档为每户每月用电量不超过 $ 240 $ 度,电价为每度 $ 0.6 $ 元；第二档为用电量超过 $ 240 $ 度但不超过 $ 400 $ 度,超过部分电价在第一档基础上每度增加 $ 0.05 $ 元；第三档为用电量超过 $ 400 $ 度,超过部分电价在第一档基础上每度增加 $ 0.3 $ 元。
(1)若某户某月用电 $ 300 $ 度,该交多少电费？
(2)设用电量为 $ x $ 度,电费为 $ y $ 元,求 $ y $ 关于 $ x $ 的函数表达式；
(3)某居民家 $ 10 $ 月份的电费为 $ 222 $ 元,请计算该居民家 $ 10 $ 月份的用电量。

答案： 解：
(1)该交183元电费.
(2)y关于x的函数表达式为$y=\begin{cases} 0.6x,x\leqslant 240, \\ 0.65x-12,240＜x\leqslant 400, \\ 0.9x-112,x＞400. \end{cases}$
(3)该居民家10月份的用电量为360度.