2025年暑假生活重庆出版社四年级语数综合A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活重庆出版社四年级语数综合A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
一、善行,我会判断。
1. 平移既可以改变图形的位置,又可以改变图形的大小。 (
2. 小数点后面添上“0”或者去掉“0”,小数的大小不变。 (
3. $25×12×4 = 25×4×12$应用了乘法交换律。 (
4. 等边三角形是轴对称图形,它有三条对称轴。 (
5. 把一张平行四边形纸剪成一个梯形,内角和变小了。 (
1. 平移既可以改变图形的位置,又可以改变图形的大小。 (
×
)2. 小数点后面添上“0”或者去掉“0”,小数的大小不变。 (
×
)3. $25×12×4 = 25×4×12$应用了乘法交换律。 (
√
)4. 等边三角形是轴对称图形,它有三条对称轴。 (
√
)5. 把一张平行四边形纸剪成一个梯形,内角和变小了。 (
×
)
答案:
1. ×;2. ×;3. √;4. √;5. ×
1. 计算$72 + 6×(35 - 27)$时,应先算(
减
)法,再算(乘
)法,最后算(加
)法,结果是(120
)。
答案:
减,乘,加,120
2. 直角三角形一个锐角是$50^{\circ}$,另一个锐角是(
40
)$^{\circ}$。
答案:
$40$
3. 一个等边三角形的周长是$48cm$,那么它的每条边长是(
16
)cm,每个角是(60°
)。
答案:
$16$;$60^{\circ}$
4. 鸡兔同笼,从上面数有8个头,从下面数有26只脚,鸡有(
3
)只,兔有(5
)只。
答案:
$3$,$5$
5. 运用运算定律,在横线上填上合适的图形或数字。
$25×43×4 = ($
$303×a = $
$25×43×4 = ($
25
$×4)×$43
$124 + 35 + 76 = ($124
$+$76
$) + 35$$303×a = $
300
$×a +$3
$×a$ $★×(▲+■) = ★×$▲
$+$★
$×$■
答案:
$25$,$43$;$124$,$76$;$300$,$3$;$▲$,$★$,$■$。
七桥问题
七桥问题是18世纪著名数学问题之一。
18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸连接起来(如图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。
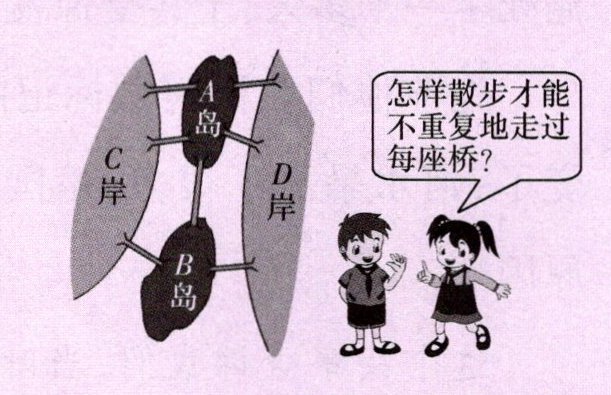
1. 首先介绍图论中的相关概念:
把陆地(包括岛和河岸)看作点,桥看作连接点的线,就构成了一个图。在图论中,与一个点相连的线的条数称为该点的度数。
对于一个能够一笔画(不重复、不遗漏地走完所有边且回到出发点)的图,需要满足的条件(欧拉定理):
图是连通的(任意两点之间都有路径相连);
每个点的度数都是偶数。
2. 然后分析七桥问题中的图:
设A、B、C、D为四个点(A、B为岛,C、D为河岸)。
计算各点的度数:假设连接A的桥有a条,连接B的桥有b条,连接C的桥有c条,连接D的桥有d条。通过观察图形可知,A、B、C、D四个点的度数都是奇数(例如,假设A与C、D、B之间有桥相连,B与A、C、D之间有桥相连等,具体桥的连接情况根据七桥实际连接情况,可算出各点度数为奇数)。
所以,按照七桥问题所构成的图,不满足一笔画(不重复、不遗漏地走完七座桥且回到出发点)的条件,即不存在这样的走法。
七桥问题是18世纪著名数学问题之一。
18世纪初普鲁士的哥尼斯堡,有一条河穿过,河上有两个小岛,有七座桥把两个岛与河岸连接起来(如图)。有个人提出一个问题:一个步行者怎样才能不重复、不遗漏地一次走完七座桥,最后回到出发点。

1. 首先介绍图论中的相关概念:
把陆地(包括岛和河岸)看作点,桥看作连接点的线,就构成了一个图。在图论中,与一个点相连的线的条数称为该点的度数。
对于一个能够一笔画(不重复、不遗漏地走完所有边且回到出发点)的图,需要满足的条件(欧拉定理):
图是连通的(任意两点之间都有路径相连);
每个点的度数都是偶数。
2. 然后分析七桥问题中的图:
设A、B、C、D为四个点(A、B为岛,C、D为河岸)。
计算各点的度数:假设连接A的桥有a条,连接B的桥有b条,连接C的桥有c条,连接D的桥有d条。通过观察图形可知,A、B、C、D四个点的度数都是奇数(例如,假设A与C、D、B之间有桥相连,B与A、C、D之间有桥相连等,具体桥的连接情况根据七桥实际连接情况,可算出各点度数为奇数)。
所以,按照七桥问题所构成的图,不满足一笔画(不重复、不遗漏地走完七座桥且回到出发点)的条件,即不存在这样的走法。
答案:
1. 首先介绍图论中的相关概念:
把陆地(包括岛和河岸)看作点,桥看作连接点的线,就构成了一个图。在图论中,与一个点相连的线的条数称为该点的度数。
对于一个能够一笔画(不重复、不遗漏地走完所有边且回到出发点)的图,需要满足的条件(欧拉定理):
图是连通的(任意两点之间都有路径相连);
每个点的度数都是偶数。
2. 然后分析七桥问题中的图:
设$A$、$B$、$C$、$D$为四个点($A$、$B$为岛,$C$、$D$为河岸)。
计算各点的度数:假设连接$A$的桥有$a$条,连接$B$的桥有$b$条,连接$C$的桥有$c$条,连接$D$的桥有$d$条。通过观察图形可知,$A$、$B$、$C$、$D$四个点的度数都是奇数(例如,假设$A$与$C$、$D$、$B$之间有桥相连,$B$与$A$、$C$、$D$之间有桥相连等,具体桥的连接情况根据七桥实际连接情况,可算出各点度数为奇数)。
所以,按照七桥问题所构成的图,不满足一笔画(不重复、不遗漏地走完七座桥且回到出发点)的条件,即不存在这样的走法。
把陆地(包括岛和河岸)看作点,桥看作连接点的线,就构成了一个图。在图论中,与一个点相连的线的条数称为该点的度数。
对于一个能够一笔画(不重复、不遗漏地走完所有边且回到出发点)的图,需要满足的条件(欧拉定理):
图是连通的(任意两点之间都有路径相连);
每个点的度数都是偶数。
2. 然后分析七桥问题中的图:
设$A$、$B$、$C$、$D$为四个点($A$、$B$为岛,$C$、$D$为河岸)。
计算各点的度数:假设连接$A$的桥有$a$条,连接$B$的桥有$b$条,连接$C$的桥有$c$条,连接$D$的桥有$d$条。通过观察图形可知,$A$、$B$、$C$、$D$四个点的度数都是奇数(例如,假设$A$与$C$、$D$、$B$之间有桥相连,$B$与$A$、$C$、$D$之间有桥相连等,具体桥的连接情况根据七桥实际连接情况,可算出各点度数为奇数)。
所以,按照七桥问题所构成的图,不满足一笔画(不重复、不遗漏地走完七座桥且回到出发点)的条件,即不存在这样的走法。
查看更多完整答案,请扫码查看


