2025年暑假生活重庆出版社四年级语数综合A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活重庆出版社四年级语数综合A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
1. 下面每组中三条线段可以围成等腰三角形的是(
A. 12 cm、4 cm、9 cm
B. 12 cm、12 cm、25 cm
C. 12 cm、6 cm、6 cm
D. 12 cm、7 cm、7 cm
D
)。A. 12 cm、4 cm、9 cm
B. 12 cm、12 cm、25 cm
C. 12 cm、6 cm、6 cm
D. 12 cm、7 cm、7 cm
答案:
D
2. 最大的内角小于$90^{\circ}$的三角形一定是(
A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 等腰三角形
C
)。A. 钝角三角形
B. 直角三角形
C. 锐角三角形
D. 等腰三角形
答案:
C
3. 聪聪在探索五边形的内角和时,把一个五边形按下图进行了分割。下面选项中,(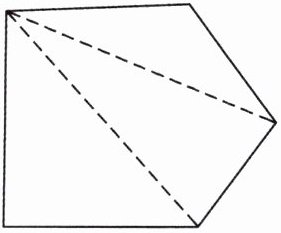
A. $180^{\circ}×3 + 360^{\circ}$
B. $180^{\circ}×5$
C. $180^{\circ}×3$
D. $180^{\circ}×5 - 180^{\circ}$
C
)体现了他的推算过程。
A. $180^{\circ}×3 + 360^{\circ}$
B. $180^{\circ}×5$
C. $180^{\circ}×3$
D. $180^{\circ}×5 - 180^{\circ}$
答案:
C
4. 下面的特性属于三角形的是(
A. 有两组对边分别平行
B. 只有一组对边平行
C. 具有稳定性
D. 有两个角是直角
C
)。A. 有两组对边分别平行
B. 只有一组对边平行
C. 具有稳定性
D. 有两个角是直角
答案:
C
1. 用5个正方体搭成一个立体图形,分别画出从前面、左面、上面看到的立体图形的形状。
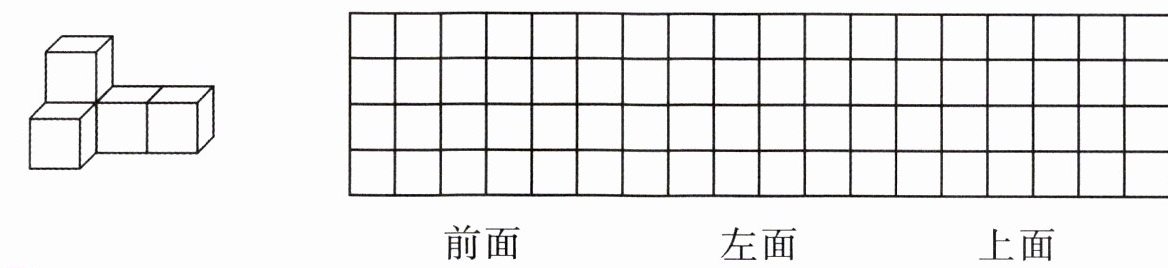

答案:

你能找到下面这些宝塔算式的秘密,并把它们补充完整吗?
1×8 + 1=
9×9+(
98×(
987×9+5=
(
98765432×9+0=
1×8 + 1=
9
9×9+(
7
)=8898×(
9
)+6=888987×9+5=
8888
(
123456789
)×8+9=98765432198765432×9+0=
888888888
答案:
1. 对于$1×8 + 1$:
计算$1×8+1=8 + 1=9$。
2. 对于$9×9+( ) = 88$:
因为$9×9 = 81$,$88−81 = 7$,所以括号里填$7$。
3. 对于$98×( )+6 = 888$:
先算$888−6 = 882$,$882÷98 = 9$,所以括号里填$9$。
4. 对于$987×9+5$:
计算$987×9+5=(1000 - 13)×9+5=(1000×9-13×9)+5=(9000 - 117)+5=8883 + 5=8888$。
5. 对于$( )×8+9 = 987654321$:
观察前面的规律,第一个因数是$123456789$,因为$123456789×8+9=(123456780 + 9)×8+9=123456780×8+9×8 + 9=987654240+72 + 9=987654321$。
6. 对于$98765432×9+0$:
计算$98765432×9+0=(100000000 - 1234568)×9=100000000×9-1234568×9=900000000-11111112 = 888888888$。
故答案依次为:$9$;$7$;$9$;$8888$;$123456789$;$888888888$。
计算$1×8+1=8 + 1=9$。
2. 对于$9×9+( ) = 88$:
因为$9×9 = 81$,$88−81 = 7$,所以括号里填$7$。
3. 对于$98×( )+6 = 888$:
先算$888−6 = 882$,$882÷98 = 9$,所以括号里填$9$。
4. 对于$987×9+5$:
计算$987×9+5=(1000 - 13)×9+5=(1000×9-13×9)+5=(9000 - 117)+5=8883 + 5=8888$。
5. 对于$( )×8+9 = 987654321$:
观察前面的规律,第一个因数是$123456789$,因为$123456789×8+9=(123456780 + 9)×8+9=123456780×8+9×8 + 9=987654240+72 + 9=987654321$。
6. 对于$98765432×9+0$:
计算$98765432×9+0=(100000000 - 1234568)×9=100000000×9-1234568×9=900000000-11111112 = 888888888$。
故答案依次为:$9$;$7$;$9$;$8888$;$123456789$;$888888888$。
2. 先在方格纸上画出对称图形的另一半,再看看分别像什么?
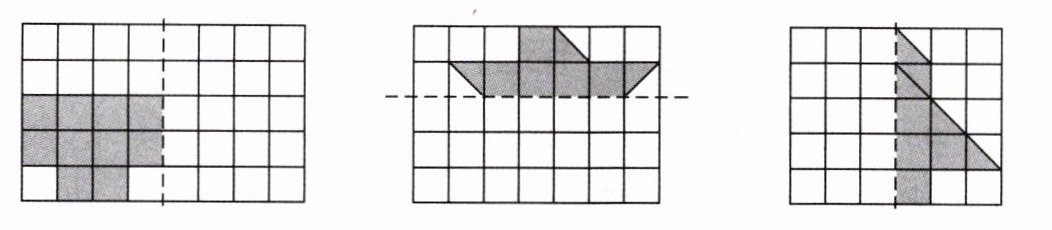

答案:

第一个图补全后像“小桌子”。
第二个图补全后像“飞机”。
第三个图补全后像“树”。
第一个图补全后像“小桌子”。
第二个图补全后像“飞机”。
第三个图补全后像“树”。
1. 荷花池的周长是
18m
,面积是15m²
;小花园的周长是22m
,面积是18m²
。
答案:
1. 计算荷花池的周长和面积:
周长**:
利用平移法,将荷花池的边平移后可发现,其周长等于边长为$5m$和$4m$的长方形的周长。
根据长方形周长公式$C=(a + b)×2$(其中$a = 5m$,$b = 4m$),则$C=(5 + 4)×2=18m$。
面积**:
用数方格的方法(不满一格按半格计算),满格有$12$个,半格有$6$个。
面积$S = 12×1+6×0.5=12 + 3=15m^{2}$。
2. 计算小花园的周长和面积:
周长**:
利用平移法,将小花园的边平移后可发现,其周长等于长为$7m$,宽为$4m$的长方形的周长。
根据长方形周长公式$C=(a + b)×2$(其中$a = 7m$,$b = 4m$),则$C=(7 + 4)×2=22m$。
面积**:
用数方格的方法(不满一格按半格计算),满格有$16$个,半格有$4$个。
面积$S = 16×1+4×0.5=16 + 2=18m^{2}$。
综上,荷花池周长$18m$,面积$15m^{2}$;小花园周长$22m$,面积$18m^{2}$。
周长**:
利用平移法,将荷花池的边平移后可发现,其周长等于边长为$5m$和$4m$的长方形的周长。
根据长方形周长公式$C=(a + b)×2$(其中$a = 5m$,$b = 4m$),则$C=(5 + 4)×2=18m$。
面积**:
用数方格的方法(不满一格按半格计算),满格有$12$个,半格有$6$个。
面积$S = 12×1+6×0.5=12 + 3=15m^{2}$。
2. 计算小花园的周长和面积:
周长**:
利用平移法,将小花园的边平移后可发现,其周长等于长为$7m$,宽为$4m$的长方形的周长。
根据长方形周长公式$C=(a + b)×2$(其中$a = 7m$,$b = 4m$),则$C=(7 + 4)×2=22m$。
面积**:
用数方格的方法(不满一格按半格计算),满格有$16$个,半格有$4$个。
面积$S = 16×1+4×0.5=16 + 2=18m^{2}$。
综上,荷花池周长$18m$,面积$15m^{2}$;小花园周长$22m$,面积$18m^{2}$。
2. 以前农村建造房屋常见的房顶结构是等腰三角形的“人字梁”。它的主要外观是由3根木料组成。下面有6根木料,请你想一想,选一选。(填序号)

(1) 选第(
(2) 第(
第(

(1) 选第(
①
)、(②
)、(③
)根木料能组成“人字梁”。
(2) 第(
③
)根木料作为“人字梁”的底边,建造的房顶要“宽”一些;第(
①
)根木料作为“人字梁”的底边,建造的房顶要“高”一些。
答案:
1. (1)
解:根据三角形三边关系“任意两边之和大于第三边,任意两边之差小于第三边”以及等腰三角形两腰相等的性质。
假设选①$3m$、②$3m$、③$4m$。
因为$3 + 3>4$,$3+4 > 3$,$4 - 3<3$,$3 - 3<4$,且有两条边相等($3m = 3m$),所以选第①、②、③根木料能组成“人字梁”(答案不唯一,也可选④$5m$、⑤$5m$、⑥$6m$等,只要满足三边关系和等腰三角形性质即可)。
2. (2)
根据三角形的面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),在等腰三角形(“人字梁”)中,当两腰(设为$b$)一定时(根据勾股定理$h=\sqrt{b^{2}-\left(\frac{a}{2}\right)^{2}}$)。
底边越长,房顶越宽;底边越短,房顶越高。
所以第③(或⑥)根木料作为“人字梁”的底边,建造的房顶要“宽”一些;第①(或④)根木料作为“人字梁”的底边,建造的房顶要“高”一些。
故答案依次为:(1)①、②、③(答案不唯一);(2)③(或⑥)、①(或④)。
解:根据三角形三边关系“任意两边之和大于第三边,任意两边之差小于第三边”以及等腰三角形两腰相等的性质。
假设选①$3m$、②$3m$、③$4m$。
因为$3 + 3>4$,$3+4 > 3$,$4 - 3<3$,$3 - 3<4$,且有两条边相等($3m = 3m$),所以选第①、②、③根木料能组成“人字梁”(答案不唯一,也可选④$5m$、⑤$5m$、⑥$6m$等,只要满足三边关系和等腰三角形性质即可)。
2. (2)
根据三角形的面积公式$S=\frac{1}{2}ah$($a$为底,$h$为高),在等腰三角形(“人字梁”)中,当两腰(设为$b$)一定时(根据勾股定理$h=\sqrt{b^{2}-\left(\frac{a}{2}\right)^{2}}$)。
底边越长,房顶越宽;底边越短,房顶越高。
所以第③(或⑥)根木料作为“人字梁”的底边,建造的房顶要“宽”一些;第①(或④)根木料作为“人字梁”的底边,建造的房顶要“高”一些。
故答案依次为:(1)①、②、③(答案不唯一);(2)③(或⑥)、①(或④)。
查看更多完整答案,请扫码查看


