2025年暑假生活重庆出版社四年级语数综合A版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活重庆出版社四年级语数综合A版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第47页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
三、善用,我会算。
计算下面各题,能简算的要简算。
$37×23 - 23×7$ $99×3.6 + 3.6$ $5.6÷4÷2.5$
计算下面各题,能简算的要简算。
$37×23 - 23×7$ $99×3.6 + 3.6$ $5.6÷4÷2.5$
答案:
690;360;0.56
1. 一个三位小数保留两位小数近似值是$2.58$,在可能的数上涂上你喜欢的颜色。 (
(
 (
(应给$2.576$和$2.583$涂上颜色。
)
答案:
应给$2.576$和$2.583$涂上颜色。
2. 学校食堂运来大米和面粉各$80$袋,大米每袋$15kg$,面粉每袋$25kg$,大米和面粉共多少千克?(请用两种方法解答)
答案:
$3200$千克
3. 用数字卡片$2$、$4$、$6和小数点.$,能组成哪些不同的两位小数?请你写出来。
答案:
$2.46$、$2.64$、$4.26$、$4.62$、$6.24$、$6.42$
找规律
黑猫警长需要一个善于观察和推理的好助手,他打算公开招聘一个助理,招聘启事中包含了这样一个题目:
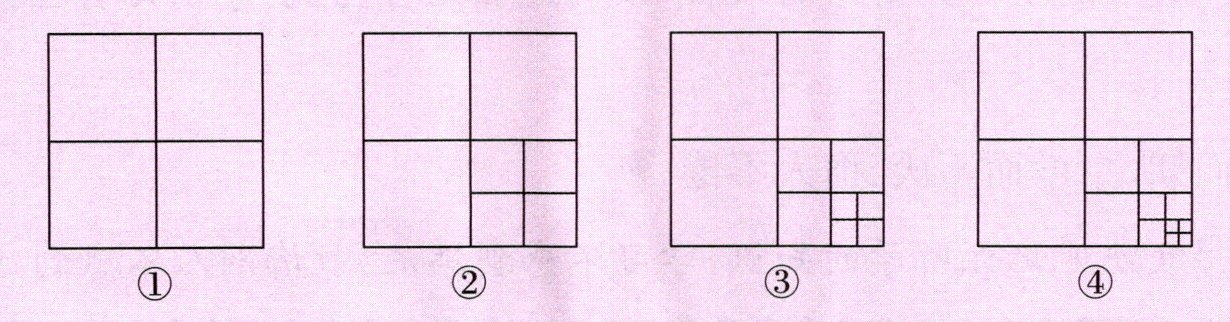
将正方形平均分成4份成了图①,共有5个正方形;再将图①中的一个小正方形平均分成4份,就成了图②,共有9个正方形;再将图②中的小正方形平均分成4份,就成了图③……
(1)图④中共有多少个正方形?
(2)这样分下去,第8个图形中共有多少个正方形?
你能解决这个问题吗?可以尝试列表解决哟!
黑猫警长需要一个善于观察和推理的好助手,他打算公开招聘一个助理,招聘启事中包含了这样一个题目:
将正方形平均分成4份成了图①,共有5个正方形;再将图①中的一个小正方形平均分成4份,就成了图②,共有9个正方形;再将图②中的小正方形平均分成4份,就成了图③……
(1)图④中共有多少个正方形?
17
(2)这样分下去,第8个图形中共有多少个正方形?
33
你能解决这个问题吗?可以尝试列表解决哟!

答案:
1. 首先列表找规律:
设图形序号为$n$,正方形个数为$a_{n}$。
当$n = 1$时,$a_{1}=5 = 4×1 + 1$;
当$n = 2$时,$a_{2}=9 = 4×2 + 1$;
当$n = 3$时,$a_{3}=13 = 4×3 + 1$;
由此可归纳出规律:$a_{n}=4n + 1$。
2. 然后求图④中正方形个数:
当$n = 4$时,根据$a_{n}=4n + 1$。
把$n = 4$代入$a_{n}=4n + 1$,得$a_{4}=4×4+1$。
计算$a_{4}=16 + 1=17$。
3. 最后求第$8$个图形中正方形个数:
当$n = 8$时,根据$a_{n}=4n + 1$。
把$n = 8$代入$a_{n}=4n + 1$,得$a_{8}=4×8+1$。
计算$a_{8}=32 + 1=33$。
综上,
(1)图④中共有$17$个正方形;
(2)第$8$个图形中共有$33$个正方形。
设图形序号为$n$,正方形个数为$a_{n}$。
当$n = 1$时,$a_{1}=5 = 4×1 + 1$;
当$n = 2$时,$a_{2}=9 = 4×2 + 1$;
当$n = 3$时,$a_{3}=13 = 4×3 + 1$;
由此可归纳出规律:$a_{n}=4n + 1$。
2. 然后求图④中正方形个数:
当$n = 4$时,根据$a_{n}=4n + 1$。
把$n = 4$代入$a_{n}=4n + 1$,得$a_{4}=4×4+1$。
计算$a_{4}=16 + 1=17$。
3. 最后求第$8$个图形中正方形个数:
当$n = 8$时,根据$a_{n}=4n + 1$。
把$n = 8$代入$a_{n}=4n + 1$,得$a_{8}=4×8+1$。
计算$a_{8}=32 + 1=33$。
综上,
(1)图④中共有$17$个正方形;
(2)第$8$个图形中共有$33$个正方形。
查看更多完整答案,请扫码查看


