《2025年新课程暑假作业广西师范大学出版社七年级数学》

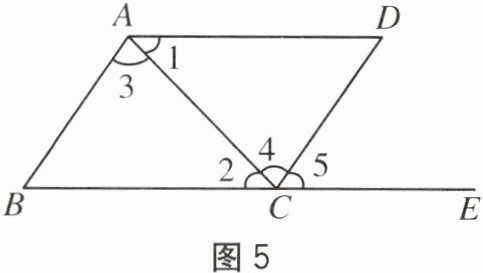
5. 如图 5,给出下列条件：① $ \angle B + \angle BCD = 180^{\circ} $；② $ \angle 1 = \angle 2 $；③ $ \angle 3 = \angle 4 $；④ $ \angle B = \angle 5 $；⑤ $ \angle B = \angle D $。其中,一定能判定 $ AB // CD $ 的条件有____(填写所有正确的序号)。

答案： ①③④

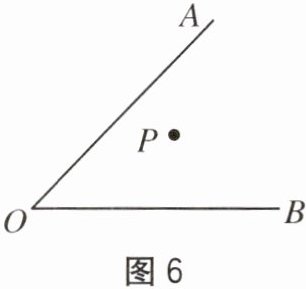
6. 如图 6,已知 $ \angle AOB $ 及 $ \angle AOB $ 内部一点 $ P $。
(1)过点 $ P $ 画直线 $ PC // OA $ 交 $ OB $ 于点 $ C $。
(2)过点 $ P $ 画垂线 $ PD \perp OB $ 于点 $ D $。
(3)猜想 $ \angle AOB $ 与 $ \angle CPD $ 的数量关系,并说明理由。

答案：
（1）如答图 4，直线 PC 即为所求 （2）如答图 4，直线 PD 即为所求 （3）猜想：$∠AOB + ∠CPD = 90^{\circ}$。理由：$\because OA // PC$，$\therefore ∠AOB = ∠PCD$。$\because PD \perp CD$，$\therefore ∠PDC = 90^{\circ}$，$\therefore ∠PCD + ∠CPD = ∠AOB + ∠CPD = 90^{\circ}$

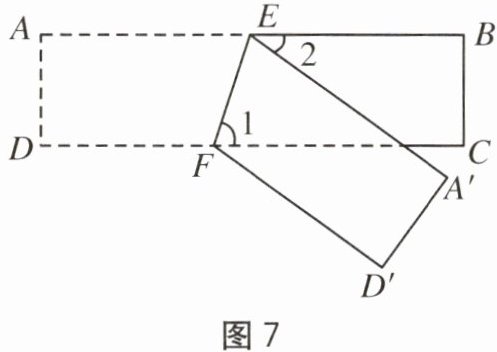
7. 如图 7,$ ABCD $ 为一长方形纸带,$ AB // CD $,将纸带沿 $ EF $ 折叠,$ A $,$ D $ 两点分别与点 $ A' $,$ D' $ 对应。若 $ \angle 1 = 2 \angle 2 $,则 $ \angle AEF $ 的度数为()。

A. $ 60^{\circ} $
B. $ 65^{\circ} $
C. $ 72^{\circ} $
D. $ 75^{\circ} $

答案： C

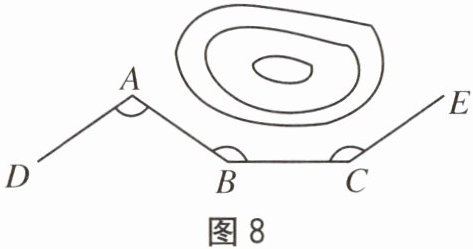
8. 如图 8,一条公路修到湖边时,需要拐弯绕湖而过,第一次拐的角 $ \angle A = 110^{\circ} $,第二次拐的角 $ \angle B = 145^{\circ} $,则第三次拐的角 $ \angle C = $____时,道路 $ CE $ 才能恰好与 $ AD $ 平行。

答案： $145^{\circ}$

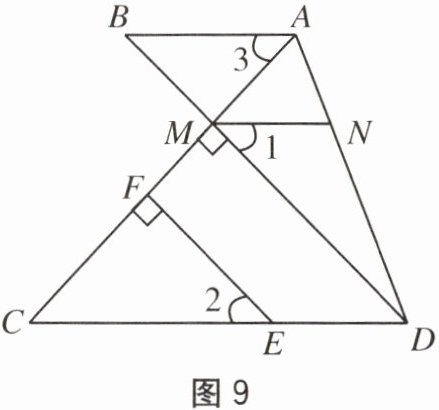
9. 如图 9,$ EF \perp AC $ 于点 $ F $,$ DB \perp AC $ 于点 $ M $,$ \angle 1 = \angle 2 $,$ \angle 3 = \angle C $。
求证：$ AB // MN $。

答案： $\because EF \perp AC$，$DB \perp AC$，$\therefore EF // DM$，$\therefore ∠2 = ∠CDM$。$\because ∠1 = ∠2$，$\therefore ∠1 = ∠CDM$，$\therefore MN // CD$，$\therefore ∠C = ∠AMN$。$\because ∠3 = ∠C$，$\therefore ∠3 = ∠AMN$，$\therefore AB // MN$