3. 为了制定更加合理的用电管理方案,某市对居民生活用电情况进行了调查,如图 5 和图 6 分别是通过抽样调查获得的若干户家庭去年的月均用电量 x(单位:$kW\cdot h$)的频数分布直方图(数据包括左端点不包括右端点)和扇形统计图.
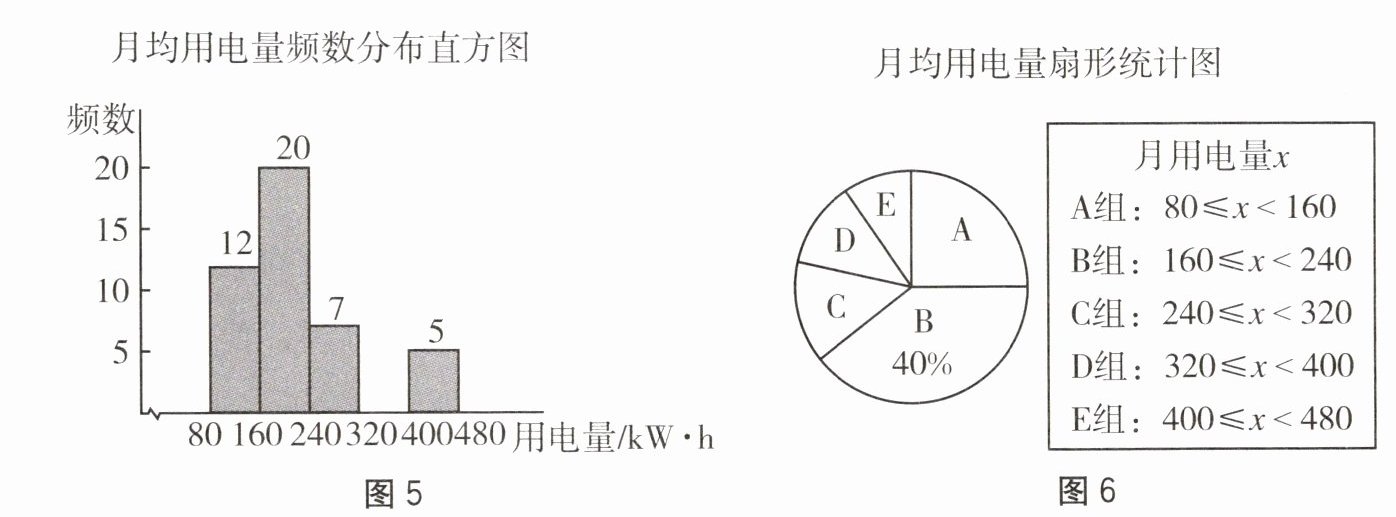
(1)本次抽样调查的样本容量是______.
(2)补全频数分布直方图.
(3)为鼓励节约用电,将原来$0.50 元/kW\cdot h$的电费标准改为按月均用电量分为三档,如下表所示.
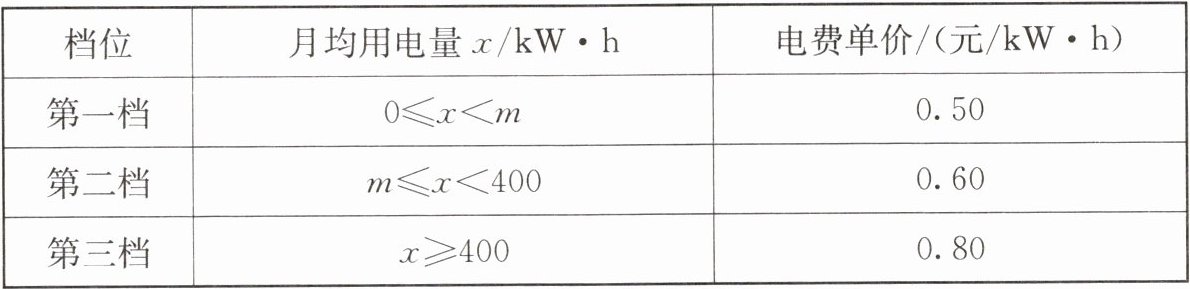
①若该市共有 250 万户家庭,试估计该市需要按第三档标准缴纳电费的家庭数.
②抽样结果中,月均用电量 x 为$240\leqslant x\lt320$的 7 个家庭,其月均用电量依次为 248,269,279,282,302,313,318. 若要使约 70%的家庭电费支出不受到影响,请写出一个合理的 m 值.

(1)本次抽样调查的样本容量是______.
(2)补全频数分布直方图.
(3)为鼓励节约用电,将原来$0.50 元/kW\cdot h$的电费标准改为按月均用电量分为三档,如下表所示.

①若该市共有 250 万户家庭,试估计该市需要按第三档标准缴纳电费的家庭数.
②抽样结果中,月均用电量 x 为$240\leqslant x\lt320$的 7 个家庭,其月均用电量依次为 248,269,279,282,302,313,318. 若要使约 70%的家庭电费支出不受到影响,请写出一个合理的 m 值.
答案:
(1) 50
(2) D 组的频数为:$50 - 12 - 20 - 7 - 5 = 6$
(3) ①$250×\frac{5}{50} = 25$(万户)
②$\because 50×70\% = 35$,$\therefore m$为$279 < m ≤ 282$的任意值皆可(答案不唯一)
(1) 50
(2) D 组的频数为:$50 - 12 - 20 - 7 - 5 = 6$
(3) ①$250×\frac{5}{50} = 25$(万户)
②$\because 50×70\% = 35$,$\therefore m$为$279 < m ≤ 282$的任意值皆可(答案不唯一)
查看更多完整答案,请扫码查看


