搜索
10. 如图7,河道$l的一侧有A$,$B$两个村庄,现要铺设一条引水管道把河水引向$A$,$B$两村,下列四种方案中最节省材料的是()．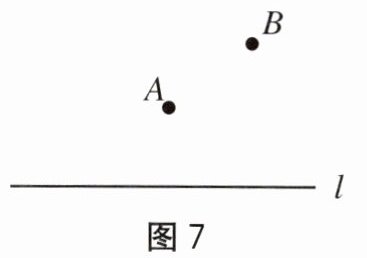
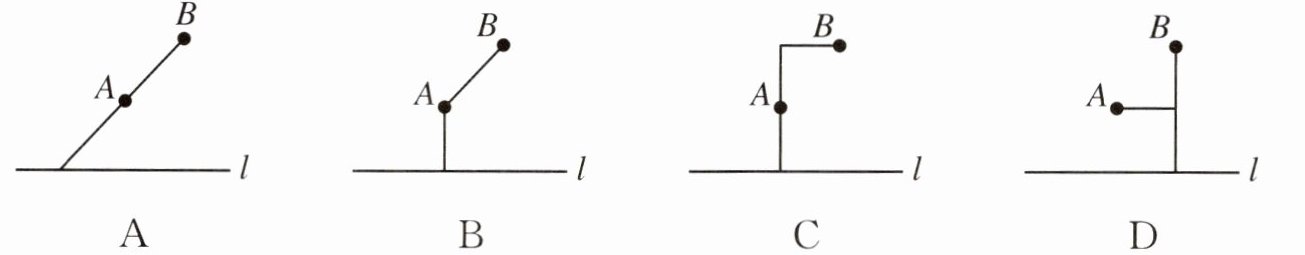
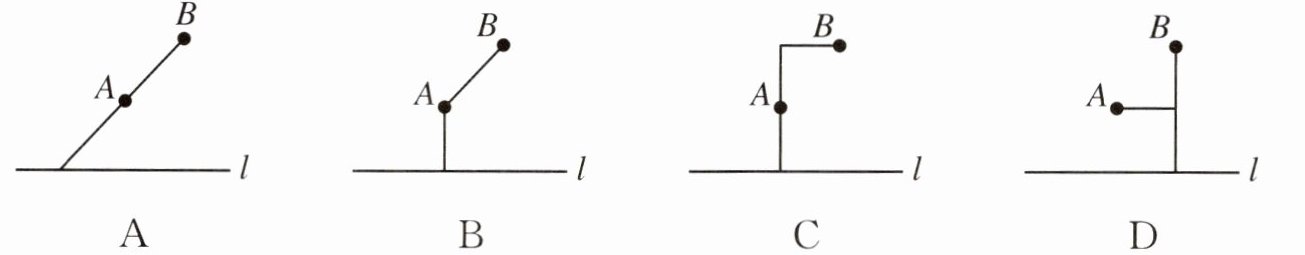
答案：
B
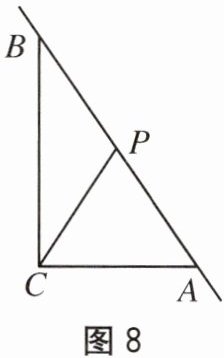
11. 如图8,在三角形$ABC$中,$∠ACB= 90^{\circ}$,$AC= 3$,$BC= 4$,$AB= 5$,$P为直线AB$上一动点,连接$PC$,则线段$PC$的最小值是()．
A. $3$
B. $2.5$
C. $2.4$
D. $2$
A. $3$
B. $2.5$
C. $2.4$
D. $2$
答案：
C
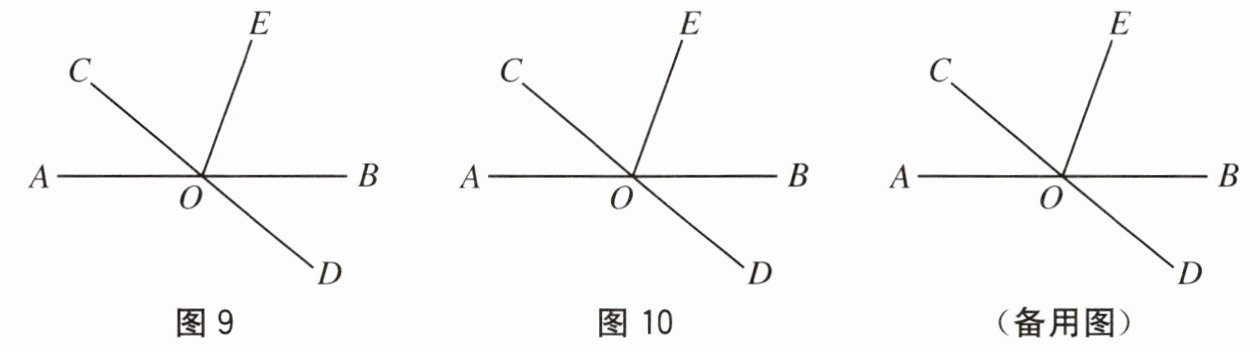
12. 如图9,直线$AB$,$CD相交于点O$,$OE平分∠BOC$．
【基础尝试】(1)如图9,若$∠AOC= 40^{\circ}$,求$∠DOE$的度数．
【画图探究】(2)作射线$OF⊥OC$,设$∠AOC= x^{\circ}$,请你利用图10画出图形,探究$∠AOC与∠EOF$之间的关系,结果用含$x的代数式表示∠EOF$．
【拓展运用】(3)在第(2)题中,$∠EOF可能和∠DOE$互补吗？请你做出判断并说明理由．
【基础尝试】(1)如图9,若$∠AOC= 40^{\circ}$,求$∠DOE$的度数．
【画图探究】(2)作射线$OF⊥OC$,设$∠AOC= x^{\circ}$,请你利用图10画出图形,探究$∠AOC与∠EOF$之间的关系,结果用含$x的代数式表示∠EOF$．
【拓展运用】(3)在第(2)题中,$∠EOF可能和∠DOE$互补吗？请你做出判断并说明理由．
答案：
(1) $110^{\circ}$
(2) $\angle EOF=\frac{1}{2}\angle AOC$ 或 $\angle EOF=180^{\circ}-\frac{1}{2}\angle AOC$。当 $OF$ 在 $\angle BOC$ 内部时，如答图 1.
$\because \angle AOC+\angle BOC=180^{\circ}$，$\angle AOC=x^{\circ}$，$\therefore \angle BOC=(180-x)^{\circ}$。$\because OE$ 平分 $\angle BOC$，$\therefore \angle COE=\frac{1}{2}\angle BOC=(90-\frac{1}{2}x)^{\circ}$。$\because OF\perp OC$，$\therefore \angle COF=90^{\circ}$，$\therefore \angle EOF=90^{\circ}-\angle COE=90^{\circ}-(90-\frac{1}{2}x)^{\circ}=\frac{1}{2}x^{\circ}$。当 $OF$ 在 $\angle AOD$ 内部时，如答图 2.
$\angle EOF=90^{\circ}+\angle COE=90^{\circ}+(90-\frac{1}{2}x)^{\circ}=(180-\frac{1}{2}x)^{\circ}$
(3) $\angle EOF$ 可能和 $\angle DOE$ 互补，如答图 3.
当 $AB\perp CD$，且 $OF$ 与 $OB$ 重合时，$\angle BOC=\angle BOD=90^{\circ}$。 $\because OE$ 平分 $\angle BOC$，$\therefore \angle BOE=\frac{1}{2}\angle BOC=45^{\circ}$，即 $\angle EOF=45^{\circ}$，$\therefore \angle DOE=\angle BOD+\angle BOE=135^{\circ}$，$\therefore \angle EOF+\angle DOE=180^{\circ}$，即 $\angle EOF$ 和 $\angle DOE$ 互补
(1) $110^{\circ}$
(2) $\angle EOF=\frac{1}{2}\angle AOC$ 或 $\angle EOF=180^{\circ}-\frac{1}{2}\angle AOC$。当 $OF$ 在 $\angle BOC$ 内部时，如答图 1.
$\because \angle AOC+\angle BOC=180^{\circ}$，$\angle AOC=x^{\circ}$，$\therefore \angle BOC=(180-x)^{\circ}$。$\because OE$ 平分 $\angle BOC$，$\therefore \angle COE=\frac{1}{2}\angle BOC=(90-\frac{1}{2}x)^{\circ}$。$\because OF\perp OC$，$\therefore \angle COF=90^{\circ}$，$\therefore \angle EOF=90^{\circ}-\angle COE=90^{\circ}-(90-\frac{1}{2}x)^{\circ}=\frac{1}{2}x^{\circ}$。当 $OF$ 在 $\angle AOD$ 内部时，如答图 2. $\angle EOF=90^{\circ}+\angle COE=90^{\circ}+(90-\frac{1}{2}x)^{\circ}=(180-\frac{1}{2}x)^{\circ}$ (3) $\angle EOF$ 可能和 $\angle DOE$ 互补，如答图 3.
当 $AB\perp CD$，且 $OF$ 与 $OB$ 重合时，$\angle BOC=\angle BOD=90^{\circ}$。 $\because OE$ 平分 $\angle BOC$，$\therefore \angle BOE=\frac{1}{2}\angle BOC=45^{\circ}$，即 $\angle EOF=45^{\circ}$，$\therefore \angle DOE=\angle BOD+\angle BOE=135^{\circ}$，$\therefore \angle EOF+\angle DOE=180^{\circ}$，即 $\angle EOF$ 和 $\angle DOE$ 互补 查看更多完整答案，请扫码查看
