《2025年新课程暑假作业广西师范大学出版社七年级数学》

15. 在平面直角坐标系中,给出如下定义：点P到x轴、y轴的距离的较小值称为点P的“短距”；当点Q到x轴、y轴的距离相等时,则称点Q为“完美点”.
(1)点$A(-3,2)$的“短距”为______.
(2)若点$B(3a-1,5)$是“完美点”,求a的值.
(3)若点$C(9-2b,-5)$是“完美点”,求点$D(-6,2b-1)$的“短距”.

答案：
(1) 2
(2)
∵点$B(3a - 1,5)$是“完美点”，
∴$|3a - 1| = 5$，
∴$3a - 1 = 5$或$3a - 1 = -5$，解得$a = 2$或$a = -\frac{4}{3}$
(3) 由题意，得$|9 - 2b| = 5$，
∴$9 - 2b = 5$或$9 - 2b = -5$，解得$b = 2$或$b = 7$。当$b = 2$时，点$D(-6,3)$。
∵$|-6| = 6$，$6 ＞ 3$，
∴“短距”为3。当$b = 7$时，点$D(-6,13)$。
∵$|-6| = 6$，$13 ＞ 6$，
∴“短距”为6。综上所述，点$D(-6,2b - 1)$的“短距”为3或6

16. 五子棋和象棋、围棋一样,深受广大棋友的喜爱.五子棋的规则是：在棋盘中,由黑方先行,轮流弈子,在任一方向(横向、竖向或斜线方向)上先连成五子者为胜.如图3是两个五子棋爱好者甲和乙的部分对弈图(甲执黑子先行,乙执白子后走),观察棋盘,以点O为原点,建立平面直角坐标系,若点A的位置记作$(8,4)$,则甲必须将棋子落在哪个位置上,才不会让乙在短时间内获胜？为什么？

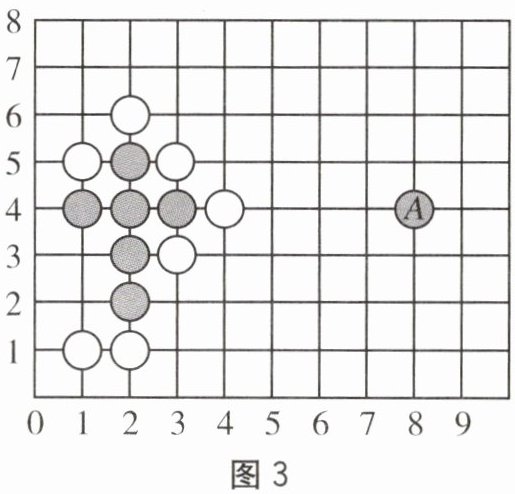
答案： 甲必须在$(1,7)$或$(5,3)$处落子。因为白棋已经有三个在一条直线上，若甲不首先截断以上两处之一，而让乙在$(1,7)$或$(5,3)$处落子，则不论截断何处，乙总有一处落子可连成五子，乙必胜无疑